Математика | Основы теории графов - набор 2

Предварительное условие - Основы теории графов - Набор 1
Граф - это структура, состоящая из набора объектов, в котором некоторые пары объектов в некотором смысле «связаны». Объекты графа соответствуют вершинам, а отношения между ними - ребрам . Граф изображен схематически как набор точек, изображающих вершины, соединенные линиями или кривыми, изображающими ребра.
Формально,

«График 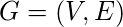состоит из 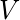, непустой набор вершин (или узлов) и 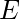, набор ребер . Каждое ребро имеет одну или две связанные с ним вершины, называемые его концами ».

Типы графов: существует несколько типов графов, которые различаются на основе ребер, их направления, веса и т. Д.

1. Простой граф . Граф, в котором каждое ребро соединяет две разные вершины и где никакие два ребра не соединяют одну и ту же пару вершин, называется простым графом. Например, рассмотрим следующий график -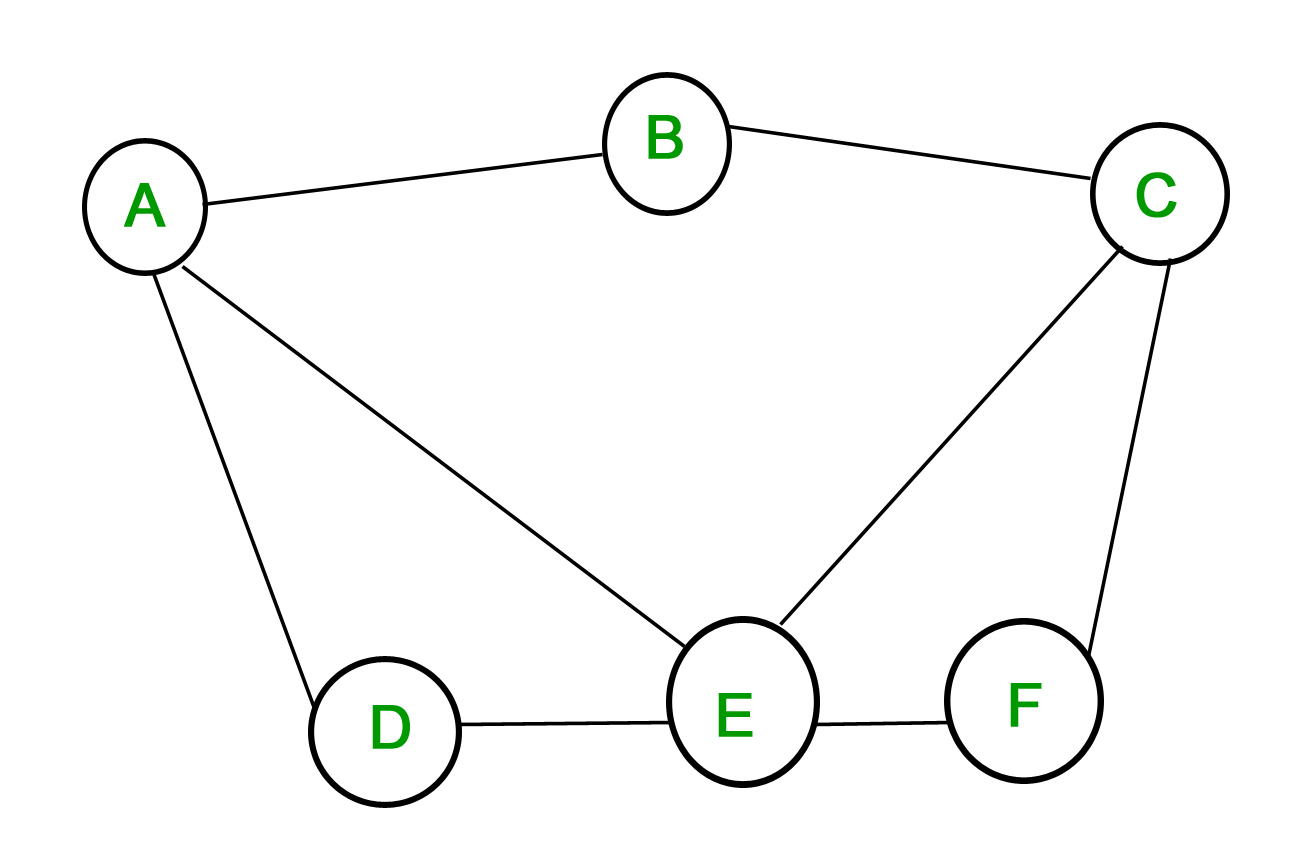

Приведенный выше граф является простым графом, поскольку ни одна вершина не имеет петли, и никакие две вершины не имеют более одного соединяющего их ребра.
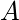Ребра обозначаются вершинами, которые они соединяют - это ребро, соединяющее вершины а также .

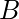2. Мультиграф . Граф, в котором несколько ребер могут соединять одну и ту же пару вершин, называется мультиграфом.
Поскольку между одной и той же парой вершин может быть несколько ребер, кратность ребра указывает количество ребер между двумя вершинами.

Приведенный выше граф является мультиграфом, поскольку между ними есть несколько ребер. 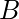а также 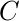. Кратность кромки равно 2.

В некоторых графах, в отличие от показанного выше, ребра ориентированы . Это означает, что отношения между объектами только односторонние, а не двусторонние. Направление краев может быть важным в некоторых приложениях.

В зависимости от того, являются ли ребра направленными или нет, мы можем иметь ориентированные графы и неориентированные графы . Это свойство может быть расширено до простых графов и мультиграфов, чтобы получить простые ориентированные или неориентированные простые графы и направленные или неориентированные мультиграфы.

Базовая терминология графа:

В приведенном выше обсуждении некоторые термины, относящиеся к графам, уже были объяснены, такие как вершины, ребра, направленные и неориентированные ребра и т. Д. Есть больше терминов, которые описывают свойства вершин и ребер.

• Смежность - в графике две вершины а также называются смежными, если они являются концами ребра. Край называется инцидентной вершинам.
  Если край направлен, считается смежным с а также называется смежным с . Здесь, называется исходной вершиной и называется конечной вершиной .
• Степень - Степень вершины - это количество ребер, инцидентных ей, за исключением петли, которая вносит двойной вклад в степень вершины. Степень вершины обозначается как .
  В случае ориентированных графов степень дополнительно классифицируется как внутренняя и исходящая . Внутренняя степень вершины - это количество ребер с данной вершиной в качестве конечной вершины. Исходная степень вершины - это количество ребер с данной вершиной в качестве начальной. In-степень обозначается как а выходная степень обозначается как .
  Например, в приведенном выше ориентированном графе, изображающем полеты между городами, входная степень вершины «Дели» равна 3, а ее исходная степень также равна 3.

Примечание: если вершина имеет нулевую степень, она называется изолированной . Если степень равна единице, то это называется подвеской .

Теорема установления связи:

Что получится, если сложить степени всех вершин графа. В случае неориентированного графа каждое ребро вносит свой вклад дважды: один раз для своей начальной вершины, а второй - для его конечной вершины. Таким образом, сумма степеней равна удвоенному количеству ребер. Этот факт утверждается в теореме о подтверждении связи.

Позволять  быть неориентированным графом с  края. потом


Если G - ориентированный граф,

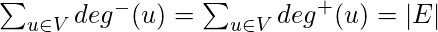
Теорема о рукопожатии для неориентированных графов дает интересный результат -

An undirected graph has an even number of vertices of odd degree.

Доказательство: Пусть а также - множества вершин четной и нечетной степеней соответственно.
Мы знаем из теоремы о рукопожатии, что,

Так,

Сумма степеней вершин с четными степенями четная. LHS также четная, что означает, что сумма степеней вершин с нечетными степенями должна быть четной.
Таким образом, число вершин с нечетной степенью четно.

Некоторые специальные простые графики:

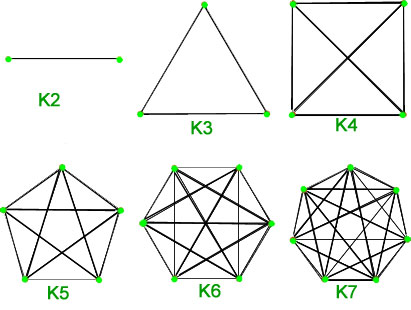
1. Полные графики - простой график 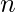вершины, имеющие ровно одно ребро между каждой парой вершин, называются полным графом. Полный график 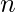вершины обозначается 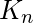. Общее количество ребер n * (n-1) / 2 с n вершинами в полном графе.

2. Циклы - Циклы - это простые графы с вершинами. и края . Цикл с 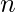вершины обозначается как 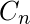. Общее количество ребер n с n вершинами в циклическом графе.

3. Колеса . Колесо похоже на цикл с одной дополнительной вершиной, которая соединена со всеми остальными вершинами. Колеса 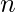вершины с 1 вершиной сложения обозначаются . Общее количество ребер 2 * (n-1) с n вершинами в колесном графе.

4. Гиперкуб . Гиперкуб или n-куб - это граф с 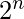вершины, каждая из которых представлена n-битной строкой. Вершины, различающиеся не более чем на 1 бит, соединены ребрами. Гиперкуб 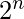вершины обозначается . Общее количество ребер n * с участием 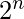вершины в графе куба.

5. Двудольные графы - простой граф называется двудольным, если его множество вершин 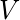можно разделить на два непересекающихся множества, так что каждое ребро в имеет начальную вершину в первом наборе и конечную вершину во втором наборе. Общее количество ребер (n * m) с (n + m) вершинами в двудольном графе.

Теорема - простой граф двудольный тогда и только тогда, когда можно сопоставить одно из двух
разные цвета для каждой вершины графа, так что никаким двум соседним не назначены
такого же цвета.

Двудольный граф с 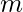а также 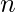вершины в его двух непересекающихся подмножествах называются полными, если есть ребро от каждой вершины в первом наборе до каждой вершины во втором наборе, всего края. Полный двудольный граф с 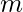вершины в первом наборе и 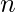вершины во втором наборе обозначаются как .

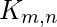Вопросы по GATE CS Corner

Выполнение следующих вопросов поможет вам проверить свои знания. Все вопросы задавались в GATE в предыдущие годы или в пробных тестах GATE. Настоятельно рекомендуется попрактиковаться в них.

1. GATE CS 2013, вопрос 25
2. GATE CS 2014 Set-1, вопрос 61
3. GATE CS 2006, вопрос 71
4. GATE CS 2002, вопрос 25
5. GATE CS 2004, вопрос 37
6. GATE CS 2014 Set-2, вопрос 13

Использованная литература-

Графики - Википедия
Дискретная математика и ее приложения, Кеннет Х. Розен

Эта статья предоставлена Чирагом Манвани . Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на deposit@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.

Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.