Максимальная площадь треугольника с разными цветами вершин
Данная матрица состоит из N строк и M столбцов, состоит из трех значений {r, g, b}. Задача состоит в том, чтобы найти площадь самого большого треугольника, у которого одна сторона параллельна оси Y, т.е. вертикальна, и цвет всех трех вершин различен.
Примеры:
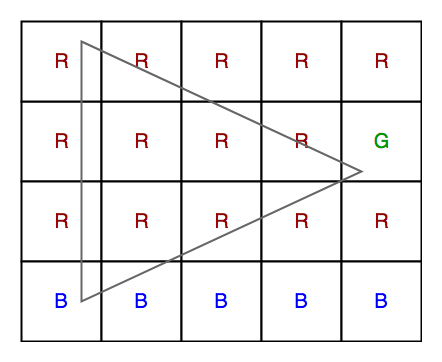
Ввод: N = 4, M = 5.
мат [] [] =
{
г, г, г, р, г,
г, г, г, г, г,
г, г, г, р, г,
б, б, б, б, б,
}
Выход: 10
Максимальная площадь треугольника 10.
Координаты треугольника: (0,0) содержит r, (1,4) содержит g, (3,0) содержит b.
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.
Мы знаем, что площадь треугольника = 1/2 * основание * высота, поэтому нам нужно максимизировать основание и высоту треугольника. Поскольку одна сторона параллельна оси Y, мы можем считать эту сторону основанием треугольника.
Чтобы максимизировать базу, мы можем найти первое и последнее вхождение {r, g, b} для каждого столбца. Итак, у нас есть два набора по 3 значения для каждого столбца. Для основания в любом столбце одна вершина берется из первого набора, а вторая вершина из второго набора, так что они имеют разные значения.
Чтобы максимизировать высоту, для любого столбца в качестве основания необходимо выбрать третью вершину так, чтобы вершина находилась дальше всего от столбца, с левой или правой стороны столбца, имеющего значение, отличное от двух других вершин.
Теперь для каждого столбца найдите максимальную площадь треугольника.
Below is the implementation of this approach:
C++
// C++ program to find maximum area of triangle// having different vertex color in a matrix.#include<bits/stdc++.h>using namespace std;#define R 4#define C 5 // return the color value so that their corresponding// index can be access.int mapcolor(char c){ if (c == "r") return 0; else if (c == "g") return 1; else if (c == "b") return 2;} // Returns the maximum area of triangle from all// the possible trianglesdouble findarea(char mat[R][C], int r, int c, int top[3][C], int bottom[3][C], int left[3], int right[3]){ double ans = (double)1; // for each column for (int i = 0; i < c; i++) // for each top vertex for (int x = 0; x < 3; x++) // for each bottom vertex for (int y = 0; y < 3; y++) { // finding the third color of // vertex either on right or left. int z = 3 - x - y; // finding area of triangle on left side of column. if (x != y && top[x][i] != INT_MAX && bottom[y][i] != INT_MIN && left[z] != INT_MAX) { ans = max(ans, ((double)1/(double)2) * (bottom[y][i] - top[x][i]) * (i - left[z])); } // finding area of triangle on right side of column. if (x != y && top[x][i] != INT_MAX && bottom[y][i] != INT_MIN && right[z] != INT_MIN) { ans = max(ans, ((double)1/(double)2) * (bottom[y][i] - top[x][i]) * (right[z] - i)); } } return ans;} // Precompute the vertices of top, bottom, left// and right and then computing the maximum area.double maxarea(char mat[R][C], int r, int c){ int left[3], right[3]; int top[3][C], bottom[3][C]; memset(left, INT_MAX, sizeof left); memset(right, INT_MIN, sizeof right); memset(top, INT_MAX, sizeof top); memset(bottom, INT_MIN, sizeof bottom); // finding the r, b, g cells for the left // and right vertices. for (int i = 0; i < r; i++) { for (int j = 0; j < c; j++) { left[mapcolor(mat[i][j])] = min(left[mapcolor(mat[i][j])], j); right[mapcolor(mat[i][j])] = max(left[mapcolor(mat[i][j])], j); } } // finsing set of {r, g, b} of top and // bottom for each column. for (int j = 0; j < c; j++) { for( int i = 0; i < r; i++) { top[mapcolor(mat[i][j])][j] = min(top[mapcolor(mat[i][j])][j], i); bottom[mapcolor(mat[i][j])][j] = max(bottom[mapcolor(mat[i][j])][j], i); } } return findarea(mat, R, C, top, bottom, left, right);} // Driven Programint main(){ char mat[R][C] = { "r", "r", "r", "r", "r", "r", "r", "r", "r", "g", "r", "r", "r", "r", "r", "b", "b", "b", "b", "b", }; cout << maxarea(mat, R, C) << endl; return 0;} |
Python3
# Python3 program to find the maximum # area of triangle having different # vertex color in a matrix. # Return the color value so that their # corresponding index can be access. def mapcolor(c): if c == "r": return 0 elif c == "g": return 1 elif c == "b": return 2 # Returns the maximum area of triangle # from all the possible triangles def findarea(mat, r, c, top, bottom, left, right): ans = 1 # for each column for i in range(0, c): # for each top vertex for x in range(0, 3): # for each bottom vertex for y in range(0, 3): # finding the third color of # vertex either on right or left. z = 3 - x - y # finding area of triangle on # left side of column. if (x != y and top[x][i] != INT_MAX and bottom[y][i] != INT_MIN and left[z] != INT_MAX): ans = max(ans, 0.5 * (bottom[y][i] - top[x][i]) * (i - left[z])) # finding area of triangle on right side of column. if (x != y and top[x][i] != INT_MAX and bottom[y][i] != INT_MIN and right[z] != INT_MIN): ans = max(ans, 0.5 * (bottom[y][i] - top[x][i]) * (right[z] - i)) return ans # Precompute the vertices of top, bottom, left # and right and then computing the maximum area. def maxarea(mat, r, c): left = [-1] * 3 right = [0] * 3 top = [[-1 for i in range(C)] for j in range(3)] bottom = [[0 for i in range(C)] for j in range(3)] # finding the r, b, g cells for # the left and right vertices. for i in range(0, r): for j in range(0, c): left[mapcolor(mat[i][j])] = min(left[mapcolor(mat[i][j])], j) right[mapcolor(mat[i][j])] = max(left[mapcolor(mat[i][j])], j) # finsing set of r, g, b of top # and bottom for each column. for j in range(0, c): for i in range(0, r): top[mapcolor(mat[i][j])][j] = min(top[mapcolor(mat[i][j])][j], i) bottom[mapcolor(mat[i][j])][j] = max(bottom[mapcolor(mat[i][j])][j], i) return int(findarea(mat, R, C, top, bottom, left, right)) # Driver Codeif __name__ == "__main__": R, C = 4, 5 mat = [["r", "r", "r", "r", "r"], ["r", "r", "r", "r", "g"], ["r", "r", "r", "r", "r"], ["b", "b", "b", "b", "b"]] INT_MAX, INT_MIN = float("inf"), float("-inf") print(maxarea(mat, R, C)) # This code is contributed by Rituraj Jain |
Выход:
10
Сложность времени: O (M * N).
Источник: http://stackoverflow.com/questions/40078660/maximum-area-of-triangle-having-all-vertices-of-different-color
Автор статьи - Анудж Чаухан (anuj0503) . Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью на сайте deposit.geeksforgeeks.org или отправить свою статью по электронной почте: grant@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.
Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .
Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.