Лексикографически наименьшая перестановка строки с заданными подпоследовательностями

Опубликовано: 16 Января, 2022

Дана строка, состоящая только из двух строчных символов 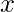а также 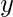и два числа 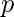а также 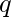. Задача состоит в том, чтобы вывести лексикографически наименьшую перестановку данной строки так, чтобы количество подпоследовательностей 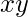является 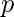и из 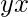является 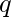. Если такой строки нет, выведите «Impossible» (без кавычек).

Примеры:

Ввод: str = "yxxyx", p = 3, q = 3 
Выход: xyxyx

Ввод: str = "yxxy", p = 3, q = 2
Выход: невозможно

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: Во-первых, с помощью индукции можно доказать, что произведение подсчета «x» и «y» должно быть равно сумме подсчета подпоследовательности «xy» и «yx» для любой данной строки. . Если это не так, то ответ - «невозможно», иначе ответ всегда существует.

Теперь отсортируйте данную строку так, чтобы счетчик подпоследовательности 'yx' стал нулевым. Пусть nx - это количество «x», а ny - количество «y». пусть a и b - количество подпоследовательностей xy и yx соответственно, тогда a = nx * ny и b = 0 . Затем с начала строки найдите «x», за которым стоит следующий «y», и поменяйте местами оба, пока не дойдете до конца строки. В каждом свопе a уменьшается на 1, а b увеличивается на 1 . Повторяйте это до тех пор, пока не будет достигнут счет подпоследовательности «yx» i: e a станет p, а b станет q .

Below is the implementation of the above approach:

C++

// CPP program to find lexicographically smallest
// string such that count of subsequence "xy" and
// "yx" is p and q respectively.
#include <bits/stdc++.h>
using namespace std;
  
// function to check if answer exits
int nx = 0, ny = 0;
  
bool check(string s, int p, int q)
{
    // count total "x" and "y" in string
    for (int i = 0; i < s.length(); ++i) {
        if (s[i] == "x")
            nx++;
        else
            ny++;
    }
  
    // condition to check existence of answer
    if (nx * ny != p + q)
        return 1;
    else
        return 0;
}
  
// function to find lexicographically smallest string
string smallestPermutation(string s, int p, int q)
{
    // check if answer exist or not
    if (check(s, p, q) == 1) {
        return "Impossible";
    }
  
    sort(s.begin(), s.end());
    int a = nx * ny, b = 0, i, j;
  
    // check if count of "xy" and "yx" becomes
    // equal to p and q respectively.
    if (a == p && b == q) {
        return s;
    }
  
    // Repeat until answer is found.
    while (1) {
        // Find index of "x" to swap with "y".
        for (i = 0; i < s.length() - 1; ++i) {
            if (s[i] == "x" && s[i + 1] == "y")
                break;
        }
  
        for (j = i; j < s.length() - 1; j++) {
            if (s[j] == "x" && s[j + 1] == "y") {
                swap(s[j], s[j + 1]);
                a--; // "xy" decrement by 1
                b++; // "yx" increment by 1
  
                // check if count of "xy" and "yx" becomes
                // equal to p and q respectively.
                if (a == p && b == q) {
                    return s;
                }
            }
        }
    }
}
  
// Driver code
int main()
{
    string s = "yxxyx";
    int p = 3, q = 3;
  
    cout<< smallestPermutation(s, p, q);
      
    return 0;
}

Java

// Java program to find lexicographically 
// smallest string such that count of 
// subsequence "xy" and "yx" is p and 
// q respectively.
import java.util.*;
  
class GFG
{
static int nx = 0, ny = 0; 
      
static boolean check(String s, 
                     int p, int q) 
{ 
    // count total "x" and "y" in string 
    for (int i = 0; i < s.length(); ++i)
    { 
        if (s.charAt(i) == "x") 
            nx++; 
        else
            ny++; 
    } 
  
    // condition to check 
    // existence of answer 
    if ((nx * ny) != (p + q)) 
        return true; 
    else
        return false; 
} 
  
public static String smallestPermutation(String s,
                                         int p, int q)
{
    if (check(s, p, q) == true) 
    { 
        return "Impossible"; 
    }
          
    char tempArray[] = s.toCharArray();
    Arrays.sort(tempArray);
      
    String str = new String(tempArray); 
    int a = nx * ny, b = 0, i = 0, j = 0;
          
    if (a == p && b == q) 
    { 
        return str; 
    }
      
    while (1 > 0) 
    { 
          
    // Find index of "x" to swap with "y". 
    for (i = 0; i < str.length() - 1; ++i)
    { 
        if (str.charAt(i) == "x" && 
            str.charAt(i + 1) == "y") 
            break; 
    } 
  
    for (j = i; j < str.length() - 1; j++) 
    { 
        if (str.charAt(j) == "x" && 
            str.charAt(j + 1) == "y") 
        { 
        StringBuilder sb = new StringBuilder(str);
        sb.setCharAt(j, str.charAt(j + 1));
        sb.setCharAt(j + 1, str.charAt(j));
        str = sb.toString();
        /* char ch[] = str.toCharArray();
            char temp = ch[j+1];
            ch[j+1] = ch[j];
            ch[j] = temp;*/
              
            a--; // "xy" decrement by 1 
            b++; // "yx" increment by 1 
  
            // check if count of "xy" and 
            // "yx" becomes equal to p 
            // and q respectively. 
            if (a == p && b == q) 
            { 
                return str; 
            } 
        } 
    } 
}
}
  
// Driver Code
public static void main (String[] args) 
{
    String s = "yxxyx"; 
    int p = 3, q = 3;
      
    System.out.print(smallestPermutation(s, p, q));
}
}
  
// This code is contributed by Kirti_Mangal

Python3

# Python3 program to find lexicographically 
# smallest string such that count of subsequence 
# "xy" and "yx" is p and q respectively. 
  
# Function to check if answer exits 
def check(s, p, q): 
      
    global nx
    global ny
      
    # count total "x" and "y" in string 
    for i in range(0, len(s)): 
        if s[i] == "x": 
            nx += 1
        else:
            ny += 1
  
    # condition to check existence of answer 
    if nx * ny != p + q: 
        return 1
    else:
        return 0
  
# Function to find lexicographically 
# smallest string 
def smallestPermutation(s, p, q): 
  
    # check if answer exist or not 
    if check(s, p, q) == 1:
        return "Impossible"
  
    s = sorted(s)
    a, b, i = nx * ny, 0, 0
  
    # check if count of "xy" and "yx" becomes 
    # equal to p and q respectively. 
    if a == p and b == q: 
        return "" . join(s) 
  
    # Repeat until answer is found. 
    while True:
          
        # Find index of "x" to swap with "y". 
        for i in range(0, len(s) - 1): 
            if s[i] == "x" and s[i + 1] == "y": 
                break
  
        for j in range(i, len(s) - 1): 
            if s[j] == "x" and s[j + 1] == "y": 
                  
                s[j], s[j + 1] = s[j + 1], s[j] 
                a -= 1 # "xy" decrement by 1 
                b += 1 # "yx" increment by 1 
  
                # check if count of "xy" and "yx" becomes 
                # equal to p and q respectively. 
                if a == p and b == q: 
                    return "" . join(s) 
  
# Driver code 
if __name__ == "__main__":
      
    nx, ny = 0, 0
    s = "yxxyx"
    p, q = 3, 3
  
    print(smallestPermutation(s, p, q)) 
      
# This code is contributed by Rituraj Jain

C#

// C# program to find lexicographically 
// smallest string such that count of 
// subsequence "xy" and "yx" is p and 
// q respectively.
using System; 
using System.Text; 
  
class GFG
{
      
static int nx = 0, ny = 0; 
      
static Boolean check(String s, 
                    int p, int q) 
{ 
    // count total "x" and "y" in string 
    for (int i = 0; i < s.Length; ++i)
    { 
        if (s[i] == "x") 
            nx++; 
        else
            ny++; 
    } 
  
    // condition to check 
    // existence of answer 
    if ((nx * ny) != (p + q)) 
        return true; 
    else
        return false; 
} 
  
public static String smallestPermutation(String s,
                                        int p, int q)
{
    if (check(s, p, q) == true) 
    { 
        return "Impossible"; 
    }
          
    char []tempArray = s.ToCharArray();
    Array.Sort(tempArray);
      
    String str = new String(tempArray); 
    int a = nx * ny, b = 0, i = 0, j = 0;
          
    if (a == p && b == q) 
    { 
        return str; 
    }
      
    while (1 > 0) 
    { 
          
    // Find index of "x" to swap with "y". 
    for (i = 0; i < str.Length - 1; ++i)
    { 
        if (str[i] == "x" && 
            str[i + 1] == "y") 
            break; 
    } 
  
    for (j = i; j < str.Length - 1; j++) 
    { 
        if (str[j] == "x" && 
            str[j + 1] == "y") 
        { 
            StringBuilder sb = new StringBuilder(str);
            sb.Remove(j,1);
            sb.Insert(j, str[j + 1]);
            sb.Remove(j+1,1);
            sb.Insert(j + 1, str[j]);
            str = sb.ToString();
            /* char ch[] = str.toCharArray();
                char temp = ch[j+1];
                ch[j+1] = ch[j];
                ch[j] = temp;*/
              
            a--; // "xy" decrement by 1 
            b++; // "yx" increment by 1 
  
            // check if count of "xy" and 
            // "yx" becomes equal to p 
            // and q respectively. 
            if (a == p && b == q) 
            { 
                return str; 
            } 
        } 
    } 
}
Алгоритмы

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Разница между жадным алгоритмом и алгоритмом «разделяй и властвуй»
14 Февраля, 2023
Сжатие и распаковка текстовых файлов с использованием кодирования Хаффмана
21 Января, 2023
Введение в амортизированный анализ
12 Января, 2023
Как анализировать сложность рекуррентного отношения
12 Января, 2023
Наихудший, средний и лучший анализ алгоритмов
4 Января, 2023
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022
Что такое логарифмическая временная сложность? Полное руководство
12 Декабря, 2022
Amazon SDE Sheet: вопросы и ответы на собеседовании
12 Декабря, 2022