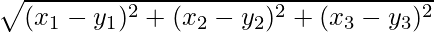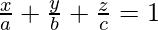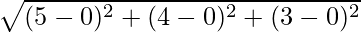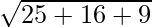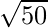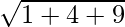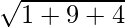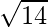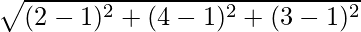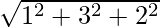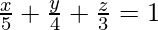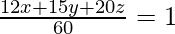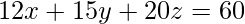Координатные оси и координатные плоскости в 3D-пространстве
Мы знаем, что на плоскости нам нужны две взаимно перпендикулярные линии, чтобы определить положение точки. Эти линии называются координатными осями плоскости, а сама плоскость обычно называется декартовой плоскостью. Но в реальной жизни у нас нет такого самолета. В реальной жизни, чтобы найти объекты, нам нужна дополнительная информация, такая как высота. Итак, теперь нам нужны три вещи, чтобы найти точку в реальной жизни — x, y и ее высота, которая обычно обозначается как z. Они называются координатами относительно трехмерного пространства.
Координатные оси и координатные плоскости
На рисунке мы видим три пересекающиеся друг с другом плоскости. Эти плоскости взаимно перпендикулярны друг другу. Линии XOX', Y'OY и Z'OZ представляют собой пересечение всех плоскостей друг с другом. Эти линии называются осью x, осью y и осью z соответственно, и они образуют прямоугольную трехмерную систему координат.

Координатные плоскости
Плоскости XOY, YOZ и ZOX называются XY-плоскостью, YZ-плоскостью и ZX-плоскостью соответственно. Пересечение всех плоскостей называется началом координат. Эти плоскости делят трехмерное пространство на 8 октантов.
Координаты точки в пространстве
Предполагается, что любая точка в трехмерном пространстве имеет три координаты, обозначающие значения координат x, y и z. На рисунке ниже нам дана точка A(x, y, z), расположенная в пространстве. Опускаем перпендикуляр из А на плоскость ху в точку М. Длина АМ дает нам значение координаты z. На рисунке LM и OL дают нам значение координаты y и x.

Таким образом, для любой точки, присутствующей в пространстве, существует упорядоченная тройка (x, y, z), которая задает положение этой точки в пространстве.
Coordinates of the origin are (0, 0, 0). A point on x-axis is of the form (x, 0, 0), same goes for the points on y-axis and z-axis.
Расстояние между двумя точками
Допустим, у нас есть две точки (x 1 , y 1 , z 1 ) и (x 2 , y 2 , z 2 ) в трехмерном пространстве. Формула для вычисления расстояния между двумя точками в трехмерном пространстве аналогична формуле Евклида для расстояния, которую мы изучили для двумерного пространства. Эта формула представляет собой небольшую модификацию исходной формулы, данной Евклидом.
The distance between two points (x1, y1, z1) and (x2, y2, z2) is given by,
Самолет
Плоскость — это двумерная плоская поверхность, простирающаяся бесконечно далеко. Это трехмерный аналог двухмерной линии и точки в одномерном пространстве. Сложно нарисовать самолет, если мы что-то пишем на бумаге, это тоже самолет. Мы пишем в самолете. На рисунке ниже показана плоскость в трехмерном пространстве.

Let’s say we have a plane, it intersects the x-axis at “a”, y-axis at “b” and the z-axis at “c”. Its equation is given by,
This is called intercept form of the equation of plane.
Примеры проблем
Вопрос 1: Допустим, у нас есть точка на оси x, каковы ее координата y и координата z?
Решение:
In the figure, the point lies on x-axis. It can be noticed that it’s coordinates for y and z are equal to zero.
Вопрос 2: Заполните пропуски:
- Оси X и Y вместе составляют _____ плоскость.
- Все координатные плоскости делят трехмерное пространство на _______ октанты.
Отвечать:
1. X and Y axis together make XY plane.
2. All the coordinates planes divide the 3-D space into eight octants.
Вопрос 3: Рассчитайте расстояние между (0,0,0) и (5,4,3).
Решение:
For the points (x1, y1, z1) and (x2, y2, z2)
Here, (x1, y1, z1) = (0,0,0) and (x2, y2, z2) = (5,,4,3). Let the distance be “l”
l =
=
=
=
= 5√2
Вопрос 4: Рассчитайте расстояние между (0,0,0) и (1,2,3).
Решение:
For the points (x1, y1, z1) and (x2, y2, z2)
Here, (x1, y1, z1) = (0,0,0) and (x2, y2, z2) = (1,2,3). Let the distance be “l”
l =
=
=
=
Вопрос 5: Рассчитайте расстояние между (1,1,1) и (2,4,3).
Решение:
For the points (x1, y1, z1) and (x2, y2, z2)
Here, (x1, y1, z1) = (1,1,1) and (x2, y2, z2) = (2,4,3). Let the distance be “l”
l =
=
=
=
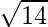
Вопрос 6: По приведенному ниже рисунку найдите уравнение плоскости.

Решение:
We know the intercept form of an equation of a plane. Let’s say we have a plane, it intersects the x-axis at “a”, y-axis at “b” and the z-axis at “c”. It’s equation is given by,
Notice in the figure, a = 5, b = 4 and c = 3
So, the equation of the plane becomes,
=
=