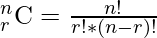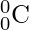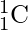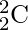Количество способов выбрать N людей, содержащих не менее 4 мальчиков и 1 девочку, из P мальчиков и Q девочек | Набор 2
Даны целые числа N, P и Q. Задача состоит в том, чтобы найти количество способов составить группу из N человек , состоящую как минимум из 4 мальчиков и 1 девочки из P мальчиков и Q девочек.
Примеры:
Input: P = 5, Q = 2, N = 5
Output: 10
Explanation: Suppose given pool is {m1, m2, m3, m4, m5} and {w1, w2}. Then possible combinations are:
m1 m2 m3 m4 w1
m2 m3 m4 m5 w1
m1 m3 m4 m5 w1
m1 m2 m4 m5 w1
m1 m2 m3 m5 w1
m1 m2 m3 m4 w2
m2 m3 m4 m5 w2
m1 m3 m4 m5 w2
m1 m2 m4 m5 w2
m1 m2 m3 m5 w2Hence the count is 10.
Input: P = 5, Q = 2, N = 6
Output: 7
Наивный подход: эта задача основана на комбинаторике , и детали наивного подхода уже обсуждались в Set-1 этой задачи.
Для некоторого общего значения P, Q и N мы можем рассчитать общее количество возможных способов, используя следующую формулу:
where
В этом подходе на каждом шаге мы вычисляли значение для каждого возможного пути.
Временная сложность: O(N 2 )
Вспомогательное пространство: O(1)
Эффективный подход: чтобы эффективно решить эту проблему, мы можем использовать свойство треугольника Паскаля для вычисления 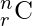 , т.е.
, т.е.
1
1 1
1 2 1
1 3 3 1
.
.
.
что не что иное, как
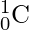
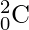
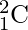
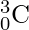
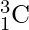
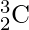
.
.
.
Выполните шаги, указанные ниже:
- Используйте треугольник Паскаля для предварительного расчета значений комбинации.
- Начните повторять цикл от i = 4 до i = P и выполняйте следующие действия для каждой итерации.
- Проверить, если (Ni) ≥ 1 и (Ni) ≤ Q .
- Если условие выполнено, то посчитаем возможные пути для i мужчин и (Ni) женщин , иначе шаг пропустить.
- Добавьте количество с общим количеством способов.
- Верните общее количество в качестве ответа.
Ниже приведена реализация подхода:
Временная сложность: O(N)
Вспомогательное пространство: O(N 2 )