Количество способов представить N как сумму простого числа и удвоенного квадрата

Опубликовано: 7 Января, 2022

Учитывая целое число N , задача состоит в том, чтобы подсчитать количество способов, чтобы N можно было записать как сумму простого числа и удвоенного квадрата, т. Е.

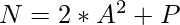
, где P может быть любым простым числом, а A - любым положительным целым числом.
Примечание:

Примеры:

Input: N = 9
Output: 1
Explanation:
9 can be represented as sum of prime number and twice a square in only one way –

Input: N = 15
Output: 2
Explanation:
15 can be represented as sum of prime number and twice a square in two ways –
[Tex]N = 15 = 13 + 2 * (1^{2}) [/Tex]

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: Идея состоит в том, чтобы использовать Seive of Eratosthenes, чтобы найти все простые числа, а затем для каждого простого числа проверять каждое возможное число, начиная с 1. Если любое простое число и дважды квадрат равны заданному числу, тогда увеличивайте счетчик числа количество путей на 1.
Ниже представлена реализация описанного выше подхода:

C++

// C++ implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square
 
#include <bits/stdc++.h>
 
using namespace std;
long long int n = 500000 - 2;
vector<long long int> v;
 
// Function to mark all the
// prime numbers using sieve
void sieveoferanthones()
{
    bool prime[n + 1];
 
    // Intially all the numbers
    // are marked as prime
    memset(prime, true,
           sizeof(prime));
 
    // Loop to mark the prime numbers
    // upto the Square root of N
    for (long long int i = 2; i <= sqrt(n);
         i++) {
        if (prime[i])
            for (long long int j = i * i;
                 j <= n; j += i) {
                prime[j] = false;
            }
    }
 
    // Loop to store the prime
    // numbers in an array
    for (long long int i = 2; i < n; i++) {
        if (prime[i])
            v.push_back(i);
    }
}
 
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
void numberOfWays(long long int n)
{
    long long int count = 0;
 
    // Loop to iterate over all the
    // possible prime numbers
    for (long long int j = 1;
         2 * (pow(j, 2)) < n; j++) {
        for (long long int i = 1;
             v[i] + 2 <= n; i++) {
 
            // Incrment the count if
            // the given number is a
            // valid number
            if (n == v[i]
+ (2 * (pow(j, 2))))
                count++;
        }
    }
    cout << count << endl;
}
 
// Driver Code
int main()
{
    sieveoferanthones();
    long long int n = 9;
 
    // Function Call
    numberOfWays(n);
    return 0;
}

Java

// Java implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square
import java.util.*;
class GFG{
 
static int n = 500000 - 2;
static Vector<Integer> v =
              new Vector<>();
 
// Function to mark all the
// prime numbers using sieve
static void sieveoferanthones()
{
  boolean []prime = new boolean[n + 1];
 
  // Intially all the numbers
  // are marked as prime
  Arrays.fill(prime, true);
 
  // Loop to mark the prime numbers
  // upto the Square root of N
  for (int i = 2;
           i <= Math.sqrt(n); i++)
  {
    if (prime[i])
      for (int j = i * i;
               j <= n; j += i)
      {
        prime[j] = false;
      }
  }
 
  // Loop to store the prime
  // numbers in an array
  for (int i = 2; i < n; i++)
  {
    if (prime[i])
      v.add(i);
  }
}
 
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
static void numberOfWays(int n)
{
  int count = 0;
 
  // Loop to iterate over all the
  // possible prime numbers
  for (int j = 1; 2 *
      (Math.pow(j, 2)) < n; j++)
  {
    for (int i = 1; v.get(i) +
             2 <= n; i++)
    {
      // Incrment the count if
      // the given number is a
      // valid number
      if (n == v.get(i) +
         (2 * (Math.pow(j, 2))))
        count++;
    }
  }
  System.out.print(count + "
");
}
 
// Driver Code
public static void main(String[] args)
{
  sieveoferanthones();
  int n = 9;
 
  // Function Call
  numberOfWays(n);
}
}
 
// This code is contributed by Princi Singh

Python3

# Python3 implementation to count the
# number of ways a number can be
# written as sum of prime number
# and twice a square
import math
 
n = 500000 - 2
v = []
 
# Function to mark all the
# prime numbers using sieve
def sieveoferanthones():
     
    prime = [1] * (n + 1)
 
    # Loop to mark the prime numbers
    # upto the Square root of N
    for i in range(2, int(math.sqrt(n)) + 1):
        if (prime[i] != 0):
             
            for j in range(i * i, n + 1, i):
                prime[j] = False
             
    # Loop to store the prime
    # numbers in an array
    for i in range(2, n):
        if (prime[i] != 0):
            v.append(i)
     
# Function to find the number
# ways to represent a number
# as the sum of prime number and
# square of a number
def numberOfWays(n):
     
    count = 0
 
    # Loop to iterate over all the
    # possible prime numbers
    j = 1
    while (2 * (pow(j, 2)) < n):
        i = 1
        while (v[i] + 2 <= n):
 
            # Incrment the count if
            # the given number is a
            # valid number
            if (n == v[i] +
               (2 * (math.pow(j, 2)))):
                count += 1
                 
            i += 1
             
        j += 1
         
    print(count)
 
# Driver Code
sieveoferanthones()
n = 9
 
# Function call
numberOfWays(n)
 
# This code is contributed by sanjoy_62

C#

// C# implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square        
using System;
using System.Collections;
using System.Collections.Generic;
 
class GFG{        
             
static int n = 500000 - 2;
 
static ArrayList v = new ArrayList();
 
// Function to mark all the
// prime numbers using sieve
static void sieveoferanthones()
{
    bool []prime = new bool[n + 1];
 
    // Intially all the numbers
    // are marked as prime
    Array.Fill(prime, true);
 
    // Loop to mark the prime numbers
    // upto the Square root of N
    for(int i = 2;
            i <= (int)Math.Sqrt(n); i++)
    {
        if (prime[i])
        {
            for(int j = i * i;
                    j <= n; j += i)
            {
                prime[j] = false;
            }
        }
    }
 
    // Loop to store the prime
    // numbers in an array
    for(int i = 2; i < n; i++)
    {
        if (prime[i])
            v.Add(i);
    }
}
 
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
static void numberOfWays(int n)
{
    int count = 0;
 
    // Loop to iterate over all the
    // possible prime numbers
    for(int j = 1;
            2 * (Math.Pow(j, 2)) < n; j++)
    {
        for(int i = 1;
           (int)v[i] + 2 <= n; i++)
        {
             
            // Incrment the count if
            // the given number is a
            // valid number
            if (n == (int)v[i] +
                     (2 * (Math.Pow(j, 2))))
                count++;
        }
    }
    Console.Write(count);
}        
         
// Driver Code        
public static void Main (string[] args)
{        
    sieveoferanthones();
    int n = 9;
 
    // Function call
    numberOfWays(n);
}        
}
 
// This code is contributed by rutvik_56

Javascript

<script>
 
// JavaScript implementation to count the
// number of ways a number can be
// written as sum of prime number
// and twice a square
 
let n = 500000 - 2;
let v = [];
  
// Function to mark all the
// prime numbers using sieve
function sieveoferanthones()
{
  let prime = Array.from({length: n+1},
                          (_, i) => true);
  
  // Loop to mark the prime numbers
  // upto the Square root of N
  for (let i = 2;
           i <= Math.sqrt(n); i++)
  {
    if (prime[i])
      for (let j = i * i;
               j <= n; j += i)
      {
        prime[j] = false;
      }
  }
  
  // Loop to store the prime
  // numbers in an array
  for (let i = 2; i < n; i++)
  {
    if (prime[i])
      v.push(i);
  }
}
  
// Function to find the number
// ways to represent a number
// as the sum of prime number and
// square of a number
function numberOfWays(n)
{
  let count = 0;
  
  // Loop to iterate over all the
  // possible prime numbers
  for (let j = 1; 2 *
      (Math.pow(j, 2)) < n; j++)
  {
    for (let i = 1; v[i] +
             2 <= n; i++)
    {
      // Incrment the count if
      // the given number is a
      // valid number
      if (n == v[i] +
         (2 * (Math.pow(j, 2))))
        count++;
    }
  }
  document.write(count + "<br/>");
}
  
  // Driver Code
     
    sieveoferanthones();
  let N = 9;
  
  // Function Call
  numberOfWays(N);
                  
</script>

Output:

Вниманию читателя! Не прекращайте учиться сейчас. Получите все важные математические концепции для соревновательного программирования с курсом Essential Maths for CP по доступной для студентов цене. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Язык программирования Олимпиады по программированию Алгоритмы

Количество способов представить N как сумму простого числа и удвоенного квадрата

C++

Java

Python3

C#

Javascript

РЕКОМЕНДУЕМЫЕ СТАТЬИ