Количество касательных из точки на окружности

Окружность — это совокупность всех точек плоскости, находящихся на постоянном расстоянии от определенной точки. Это расстояние называется радиусом окружности, а неподвижная точка называется центром. Прямая линия и окружность могут сосуществовать тремя способами, одна может быть прямой линией без пересечения с окружностью круга, всегда существует некоторое пространство между окружностью и линией. Второй тип — это когда линия проходит так, что касается окружности окружности, известной как касательные окружности. Третий тип — это когда линия пересекает окружность в двух местах и называется секущей. Они показаны ниже,

1. Нет пересечения
2. Тангенс
3. секанс

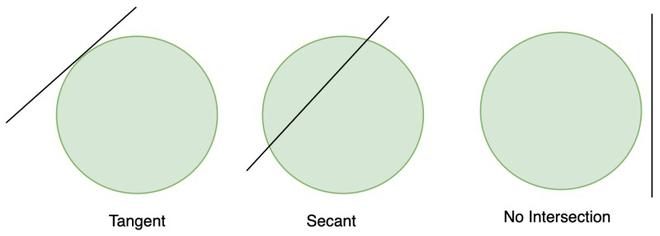
Секущая пересекает окружность в двух точках, а касательная только в одной. Давайте подробно изучим касательные и их свойства.

Касательные

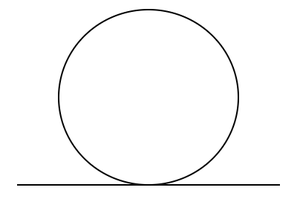
Прямая, пересекающая окружность только в одной точке, называется касательной. Окружность имеет бесконечно много возможных касательных. Общая точка касательной и окружности называется точкой касания.

Давайте посмотрим на некоторые свойства касательных через теоремы.

Количество касательных от точки к окружности

Уже известно, что касательная определяется как линия, которая проходит, касаясь окружности окружности. Чтобы получить представление об этом, нам нужно провести несколько экспериментов. Есть три случая, которые можно получить с помощью различных экспериментов.

Случай 1: Касательная внутри круга

Попробуем провести касательную внутри круга. Предположим, что точка P находится внутри круга и попробуем провести касательные. Заметим, что невозможно провести касательные внутри круга.

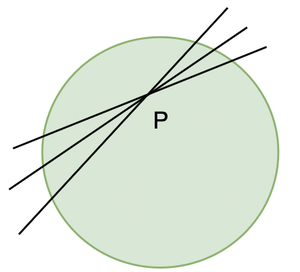
Случай 2: точка на окружности

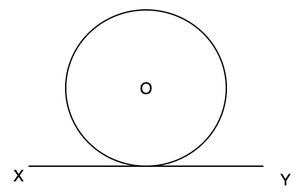
Мы видим, что на рисунке в начале статьи мы можем провести касательную из любой точки окружности. На самом деле, на окружности может быть бесконечное количество касательных.

Случай 3: точка вне круга

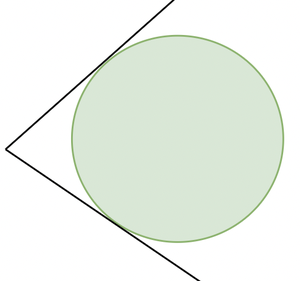
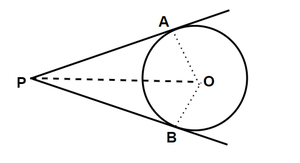
На рисунке видно, что из точки вне круга можно провести к ней две касательные.

Итак, резюмируя оба случая:

1. Не существует касательной к окружности из точки внутри окружности.
2. Существует одна касательная к окружности из точки, лежащей на окружности.
3. Возможны две касательные к окружности из точки, находящейся вне окружности.

Свойства касательных

Теорема 1:

The tangent at any point of a circle is perpendicular to the radius through the point of contact. 

Доказательство:

Let’s assume a circle with centre O and a tangent XY to circle. 

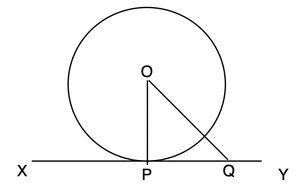
Let’s assume any point Q on the line XY and join the point of contact with centre. The diagram will look like this, 

Now the point Q when joined to centre forms OQ, if it is extended it will become a secant not tangent. Now we can see that, 

OQ > OP 

This is true when Q is any point on the line XY except the point of contact (P). P is the point on line XY whose distance is shortest from the centre O. Thus, OP must be perpendicular to XY. 

Hence, Proved. 

Эта теорема позволяет нам заключить и некоторые другие свойства:

1. В любой точке окружности может быть только одна касательная.
2. Линия, соединяющая точку контакта и центр, перпендикулярна касательной. Поэтому ее также называют нормальной к касательной.

Теорема 2:

A line drawn through the end of the radius and perpendicular to it is a tangent to the circle. 

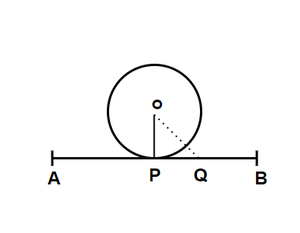
Доказательство:

Let’s assume a circle with centre O in which OP is the radius. A line AB goes through P such OP is perpendicular to AB. 

Now, take a point Q online AB. We know that the distance of Q is shortest from O when Q = P. In every other case,

OQ > OP and Q lies outside the circle. That means AB meets the circle at only one point P. Thus AB is tangent to the circle. 

Вопрос 1: На схеме, приведенной ниже. Из внешней точки, удаленной от центра на 41 см, проведены две касательные. Радиус круга равен 9 см. Найдите площадь четырехугольника AOBC.

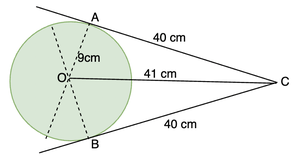
Решение:

We know from the previous theorem that line joining the centre from point of contact is perpendicular to the tangent. This makes OAC and OBC right-angled triangles. 

So now,

Area of quadrilateral AOBC = Area of triangle AOC + Area of triangle BOC. 

Area of triangle AOC =  sq units. 

Since both the triangles are congruent, both have the same area. Thus, area of BOC = 180 sq units.

Area of quadrilateral AOBC = 180 + 180 

                                            = 360 sq units. 

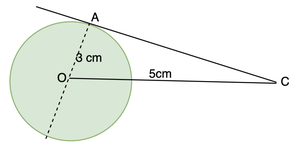
Вопрос 2. Предположим, что в точке А окружности есть касательная АВ, радиус которой равен 3 см. Расстояние от точки В до центра О равно 5 см. Найдите длину АВ.

Решение:

This is also an application of the theorem studied above, let’s make a diagram first. 

We can see a right-angled triangle AOC here ,

OC² = OA² + AC² 

52 = 32 + AC² 

25 = 9 + AC²

16 = AC²

AC = 4cm 

Теорема 3:

The lengths of tangents drawn from an external point to a circle are equal.

Доказательство:

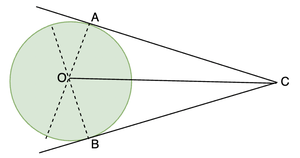
Let’s assume a circle with centre O, a point C lying outside the circle and the tangents from that point to the circle. AC and BC are the tangents from the point. Our goal is to prove AC = BC.

Let’s join OA and OB and consider the two triangles OAC and OBC. 

1. OC is common.
2. ∠OAC = ∠OBC (Right angled triangle)
3. OA = OB (Radii of the circle)

Using RHS property we can say that these two triangles are congruent. Thus, AC = BC. 

Теорема 4:

If two tangents are drawn from an external point then

1. They subtend an equal angle at the centre, and 
2. They are equally inclined to the line segment joining the centre to that point. 

Доказательство:

In the given figure, we need to prove that 

∠POA = ∠POB and ∠OPA = ∠OPB.

Let us consider the two triangles, POA and POB. 

PA = PB (By previous theorem) 

OA = OB (radii of the circle) 

OP = OP (Common) 

Thus, these two triangles are congruent. [by SSS] 

Hence, ∠POA = ∠POB and ∠OPA = ∠OPB.

Примеры проблем

Вопрос 1: На данном рисунке AC и BC — две касательные, проведенные из точки C. Докажите, что 2∠OAB = ∠ACB.

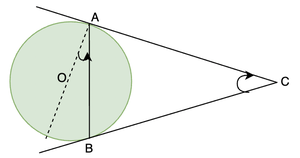
Решение:

We know from the previous theorem that, AC = BC. This concludes that triangle ABC is an isosceles triangle. 

We also know that ∠OAC = 90°. So, 

∠BAC = 90° – ∠OAB

In triangle BAC

∠BAC + ∠ABC + ∠ACB = 180°

2∠BAC + ∠ACB = 180°

2(90° – ∠OAB) + ∠ACB = 180°

180° – 2∠OAB + ∠ACB = 180°

∠ACB = 2∠OAB 

Вопрос 2: В четырехугольник PQRS вписана окружность. Докажите, что PQ + RS = PS + QR.

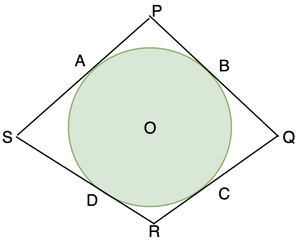
Решение:

A circle is inscribed inside the quadrilateral PQRS. Notice that the sides of the quadrilateral are actually tangents to the circle. 

PA = PB, 

BQ = QC 

DR = RC 

SA = SD 

We need to prove PQ + RS = PS + QR.

Taking the L.H.S, 

PQ + RS 

⇒ PB + BQ + DR + DS 

⇒ PA + CQ + RC + AS (From the relations stated above)

⇒ (PA + AS) + (CQ + RC) 

⇒ PS + QR 

Hence Proved

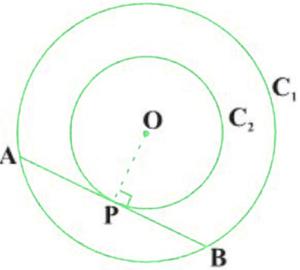
Вопрос 3: В концентрических окружностях докажите, что хорда большей окружности, которая касается меньшей окружности, делится пополам в точке касания.

Отвечать:

Let’s say C₁ and C₂ are two concentric circles. Centre is O and AB is the chord of larger circle. From the previous theorems we know that, OP is perpendicular to AB. As we know from the properties of circle, that perpendicular from the centre bisects the chord. 

AB is chord to larger circle C₁ and OP is perpendicular to it. Thus is bisects the chord.