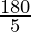Класс 9 RD Sharma Solutions – Глава 8 Введение в линии и углы – Упражнение 8.4 | Набор 2
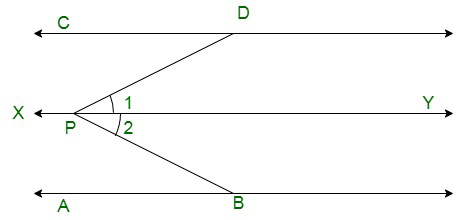
Вопрос 11. На данном рисунке прямые AB и CD параллельны, а P — любая точка, показанная на рисунке. Покажите, что ∠ABP+ ∠CDP= ∠DPB.
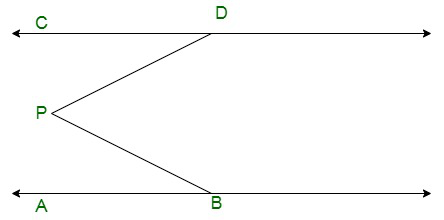
Решение:
Here in the given figure:
Given:
AB || CD
Now draw a line XY passing through point P and parallel to AB and CD.
Here,XY || CD, thus, ∠CDP and ∠1are alternate interior opposite angles. Therefore,
∠1 = ∠CDP ……(i)
Similarly, we have XY || AB, thus, ∠ABP and∠2are alternate interior opposite angles. Therefore,
∠2 = ∠ABP ….(ii)
On adding (i) and (ii)
∠1 + ∠2 = ∠CDP + ∠ABP
∠DPB = ∠CDP + ∠ABP
Thus proved.
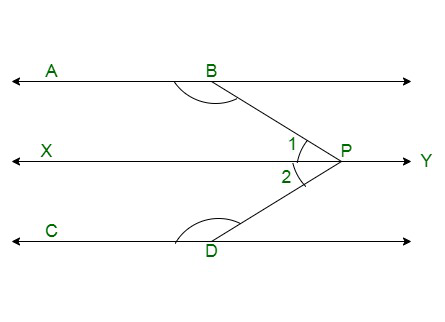
Вопрос 12. На данном рисунке AB||CD и P — любая точка, изображенная на рисунке. Докажи это:
∠АД+ ∠БДД+ ∠КДД= 360°
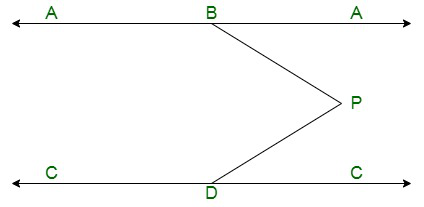
Решение:
The given figure is as follows:
It is give that AB || CD
Let us draw a line XY passing through point P and parallel to AB and CD.
We have XY || CD, thus, ∠CDP and∠2are consecutive interior angles. Therefore,
∠2 + ∠CDP = 180° ……(i)
Similarly, we have XY || AB, thus,∠CDP and∠2 are consecutive interior angles. Therefore,
∠1 + ∠ABP = 180° ……(ii)
On adding equation (i) and (ii), we get:
∠2 + ∠CDP + ∠1 + ∠ABP = 180° + 180°
(∠2 + ∠1) + ∠CDP + ∠ABP = 360°
∠ABP + ∠BPD + ∠CDP = 360°
Hence proved.
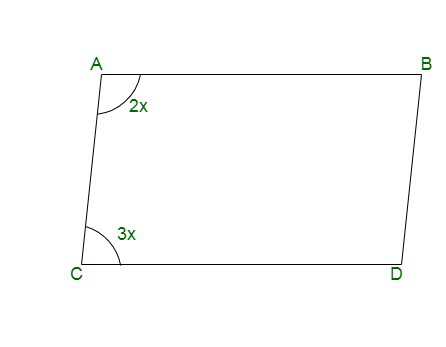
Вопрос 13. Два неравных угла параллелограмма относятся как 2 : 3. Найдите все его углы в градусах.
Решение:
The parallelogram can be drawn as follows:
It is given that
∠A : ∠C = 2 : 3
Therefore, let:
∠A = 2x and ∠C = 3x
We know that opposite angles of a parallelogram are equal.
Therefore,
∠A = ∠D
∠D = 2x
Similarly
∠B = 3x
Also, if AB || CD, then sum of consecutive interior angles is equal to180°. .
Therefore,
∠A + ∠C = 180°
2x + 3x = 180°
5x = 180°
x =
x = 36°
We have
∠A = 2x
∠A = 2(36°)
∠A = 72°
Also,
∠C = 3x
∠C = 3(36°)
∠C = 108°
Similarly,
∠D = 72°
And
∠B = 108°
Hence, the four angles of the parallelogram are as follows:
∠A = 72°, ∠B = 108°, ∠C = 72° and ∠D = 108°
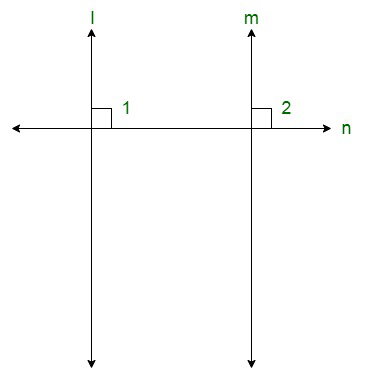
Вопрос 14. В каждой из двух прямых перпендикулярна одна и та же прямая, какие прямые относятся друг к другу?
Решение:
The figure can be drawn as follows:
Here, l ⊥ n and m ⊥n.
We need to find the relation between lines l and m
It is given that l ⊥n, therefore,
∠1 = 90° …….(i)
Similarly, we have m ⊥n, therefore,
∠2 = 90° …….(ii)
From (i) and (ii), we get:
∠1 = ∠2
But these are the pair of corresponding angles.
Theorem states: If a transversal intersects two lines in such a way that a pair of corresponding angles is equal, then the two lines are parallel.
Thus, we can say that l || m
Hence, the lines are parallel to each other.
Вопрос 15. На данном рисунке ∠1 = 60° и ∠2 =(23)rd23rd прямого угла. Докажите, что l||m.
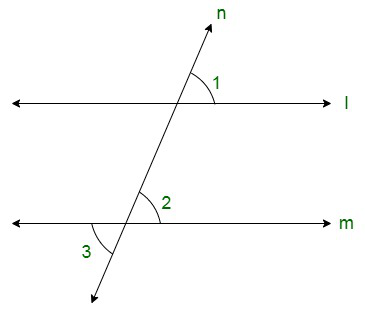
Решение:
The figure is given as follows:
It is given that ∠1 = 60°
Also,
∠2 =
(90°)
∠2 = 2(30°)
∠2 = 60°
Thus, we have ∠1 = ∠2
But these are the pair of corresponding angles.
Thus, l || m
Hence, proved.
Вопрос 16. На данном рисунке, если l||m||n и ∠1 = 60°, найти ∠2.
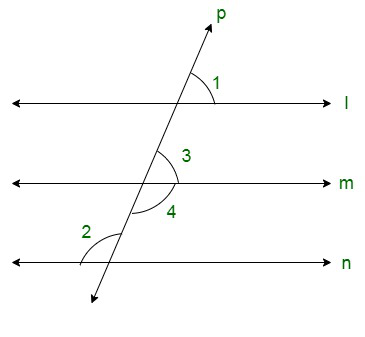
Решение:
The given figure is as follows:
We have l || m || n and ∠60°
Thus, we get ∠1 and ∠3 as corresponding angles.
Therefore,
∠3 = ∠1
∠3 = 60° ……….(i)
We have ∠3 and ∠4 forming a linear pair.
Therefore, they must be supplementary. That is;
∠3 + ∠4 = 180°
From equation (i)
60° + ∠4 = 180°
∠4 = 180° – 60°
∠4 = 120° ……(ii)
We have m || n
Thus, we get ∠2 and ∠4 as alternate interior opposite angles.
Therefore, these must be equal. That is,
∠2 = ∠4
From equation (ii), we get :
∠2 = 120°
Hence, the required value for ∠2 is 120°
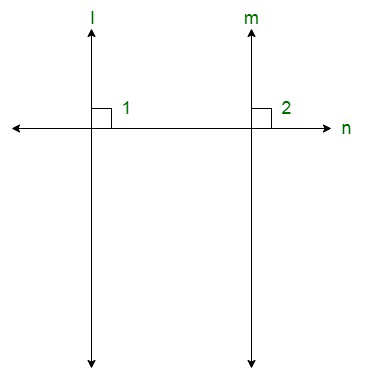
Вопрос 17. Докажите, что прямые, перпендикулярные одной и той же прямой, параллельны друг другу.
Решение:
The figure can be drawn as follows:
Here, l ⊥ m and m ⊥ n.
We need to prove that l || m
It is given that l ⊥n, therefore,
∠1 = 90° …..(i)
Similarly, we have m ⊥ n, therefore,
∠2 = 90° ……(ii)
From (i) and (ii), we get
∠1 = ∠2
But these are the pair of corresponding angles.
Theorem states: If a transversal intersects two lines in such a way that a pair of corresponding angles is equal, then the two lines are parallel.
Thus, we can say that l || m.
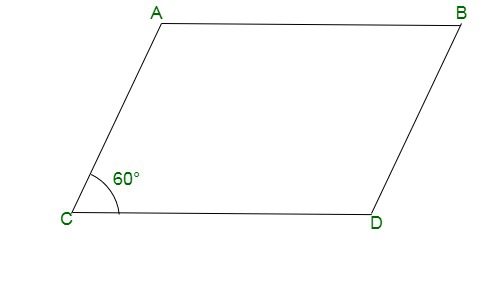
Вопрос 18. Противоположные стороны четырехугольника параллельны. Найдите остальные углы, если один из углов четырехугольника равен 60°.
Решение:
The quadrilateral can be drawn as follows:
Here, we have AB || CD and AC || BD.
Also, ∠ACD = 60°.
Thus, AB || CD.
Thus, ∠ACD and ∠BAC are consecutive interior angles.
Therefore, these two must be supplementary. i.e.
∠ACD + ∠BAC = 180°
60° + ∠BAC = 180°
∠BAC = 180° – 60°
∠BAC = 120°
Similarly, AC || BD .
Hence, ∠ACD and ∠CDB are consecutive interior angles.
Therefore, these two must be supplementary. i.e.
∠ACD + ∠CDB = 180°
60° + ∠CDB = 180°
∠CDB = 180° + 60°
∠CDB = 120°
Similarly, AB || CD.Thus, ∠ABD and ∠CDB are consecutive interior angles.
Therefore, these two must be supplementary. i.e.
∠ABD + ∠CDB = 180°
∠ABD + 120° = 180°
∠ABD = 180° – 120°
∠ABD = 60°
Thus, the other angles are as follows:
∠BAC = 120°
∠CDB = 120°
∠ABD = 60°
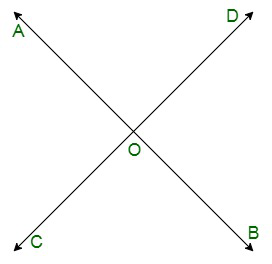
Вопрос 19. Две прямые AB и CD пересекаются в точке O. Если ∠AOC+ ∠COB+ ∠BOD= 270°, найдите меры ∠AOC, ∠COB, ∠BOD и ∠DOA.
Решение:
Since, lines AB and CD intersect each other at point O.
Thus, ∠AOC and ∠BOD are vertically opposite angles.
Therefore,
∠AOC = ∠BOD …… (i)
Similarly,
∠COB = ∠AOD …… (ii)
Also, we have ∠AOC, ∠BOD, and ∠AOD forming a complete angle.
Therefore, ∠AOC + ∠BOD + ∠COB + ∠AOD = 360°
Given:
∠AOC + ∠COB + ∠BOD = 270°
Hence, we get
(∠AOC + ∠BOD + ∠COB) + ∠AOD = 360°
270° + ∠AOD = 360°
∠AOD = 360° – 270°
∠AOD = 90°
From (ii), we will get;
∠COB = 90°
As we know that ∠AOC and ∠COB form a linear pair. Therefore, these must be supplementary.
∠AOC + ∠COB = 180°
∠AOC + 90° = 180°
∠AOC = 180° – 90°
∠AOC = 90°
From (i), we get;
∠BOD = 90°
Вопрос 20. На данном рисунке p является секущей к прямым m и n, ∠2 = 120° и ∠5 = 60°. Докажите, что m||n.
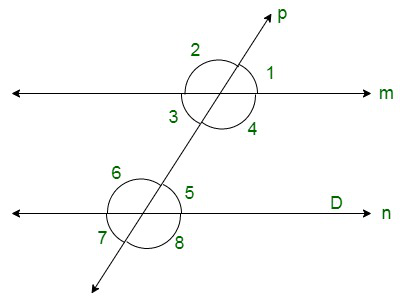
Решение:
The given figure is;
Here we have that p is a transversal to lines m and n.
Also,
∠2 = 120° and ∠5 = 60°.
To prove: m || n
Here we have ∠2 = 120°.
Also, ∠2 and ∠4 are vertically opposite angles, therefore, these two must be equal. i.e.
∠4 = 120° ……(i)
Also, ∠5 = 60°
Adding this equation to (i), we will get :
∠4 + ∠5 = 120° + 60°
∠4 + ∠5 = 60°
But these are the consecutive interior angles.
Theorem states: If a transversal intersects two lines in such a way that a pair of consecutive interior angles is supplementary, then the two lines are parallel.
Thus, m || n.
Therefore, the lines are parallel to each other.