Кэшировать забывчивый алгоритм

Cache oblivious — это способ достижения алгоритмов, эффективных в произвольных иерархиях памяти, без использования сложных многоуровневых моделей памяти. Алгоритмы забывания кэша — это алгоритмы, которые используют асимптотически оптимальные объемы работы, асимптотически оптимально перемещают данные между несколькими уровнями кэша и косвенно используют кэш процессора.

В этой статье основное внимание уделяется обсуждению следующих тем:

• Что такое алгоритм Cache Oblivious
• Кэшировать забывчивую модель.
• Обоснование Cache Oblivious модели.
• Зачем использовать алгоритм Cache-Oblivious?
• Успенский высокий тайник.
• Пример алгоритма Cache Oblivious.

Кэшировать забывчивую модель

Модели Cache Oblivious построены таким образом, что они могут быть независимыми от постоянных факторов, таких как размер кэш-памяти.

Функции:

• Он разработан для иерархии памяти, которая разделяет память компьютера на иерархию на основе времени отклика. Алгоритмы забывания кеша являются асимптотическими только тогда, когда они игнорируют постоянные факторы.
• Понятие «не обращая внимания на кеш» заключается в разработке алгоритмов и структур данных, эффективных для кэша и диска .
• Алгоритмы, не обращающие внимания на кэш, хорошо работают в многоуровневой иерархии памяти , не зная никаких параметров иерархии, но осознавая их существование. Это означает, что им просто нужно игнорировать постоянные факторы, чтобы работать эффективно.
• Существует множество способов реализации алгоритмов, не обращающих внимания на кэш, один из них — с помощью перестановки матриц, которые затем сортируются с помощью различных методов сортировки.

Обоснование модели

Модель Cache Oblivious можно обосновать на основании следующих моментов:

Модель внешней памяти

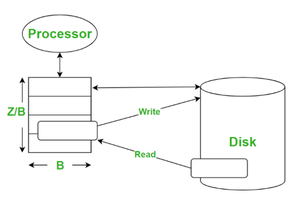
• Показанная ниже модель имеет двухуровневую иерархию памяти , состоящую из кеша (Z) и блоков данных (B), которые передаются между кешем и диском. Диск разбивается на блоки элементов B, и при доступе к одному из них на диске копируется весь его блок в кеш.
• Кэш очень близок к ЦП и имеет ограниченное пространство, диск находится далеко от ЦП и требует больших затрат с технической точки зрения. И в нем много места.
• Время доступа имеет большое значение между кешем и диском. Общая идея операции чтения заключается в чтении ранее сохраненных данных. и операция записи сохраняет новое значение в памяти. Но что происходит, когда ЦП или процессор обращается к ячейке памяти, если этот блок данных уже находится в кеше, то это называется попаданием в кеш, стоимость кеша для доступа к нему равна 0. И если он не в кеше уже, то это кеш-промах. Затем к этой памяти обращаются с диска и переносят в кеш (Z). В этом случае стоимость кэша будет равна 1.

Ассоциативный кэш:

• Кэш обычно различают по трем факторам:
  • Ассоциативность (A) - Ассоциативность A определяет номер. различных кадров или строк (B), находящихся в основной памяти. Если блок из основной памяти (Диска) может находиться в любом кадре или строке, то ассоциативность полностью выполняется.
  • Блок (B) - блок является частью минимального размера доступа к памяти.
  • Емкость (C) - Емкость является частью минимального размера доступа к памяти.
• Кэш равен C байт. Но из-за физического принуждения кеш разбивается на кадры кеша размером B. Эти факторы могут влиять на конкретный кеш.
• Когда адрес памяти отсутствует в кеше ( cache-miss ), мы должны поместить блок или строку в кеш, и он должен решить, куда его следует отобразить в кеше. Модель кэша предполагает, что любая строка или блок кэша может быть сопоставлена с любым местом в кэш-памяти. Большинство кэшей 2-х, 4-х, 8-ми, 16-ти ассоциативные.
• Что такое множественно-ассоциативное отображение?
  • Это сопоставление определенного блока основной памяти (в нашем случае диска) с набором кэшей. Это происходит, когда происходит промах кеша.
  • Строки кэша собираются в наборы, каждый из которых содержит k строк.
  • Затем блок основной памяти сопоставляется с набором кеша. Мы можем сопоставить любую свободно доступную кэш-строку из основной памяти.
  • Набор кеша, на который может быть отображена уникальная основная память, определяется как:
    

    Cache set number = [Main Memory block address] modulo [number of sets in the cache] 

Оптимальная политика замены кэша:

• Когда происходит промах кэша, новая строка кэша отображается из основной памяти в кэш.
• Но перед выборкой блока из основной памяти, если кеш уже заполнен, должен быть способ вытеснить текущую существующую строку из кеша. На самом деле оптимальной замены не существует, потому что она требует от нас знания будущего промаха кеша, который непредсказуем. Тем не менее, оптимальная политика замены кеша может быть похожа на реальную политику и может быть сделана более предсказуемой с помощью алгоритма Белади, алгоритма «первым прибыл — первым обслужен» (FIFO), «последним пришел — первым обслужен» (LIFO), наименее недавно использованным (LRU) и т. д.

Зачем использовать алгоритм Cache-Oblivious?

• Модель «забвения кеша» изобретена для того, чтобы структура данных могла отражать некоторые свойства сознания кеша.
• Алгоритм Cache Oblivious наследует некоторые свойства регистровых машин, которые обычно состоят из небольшого объема быстрой памяти и модели машины с произвольным доступом.
• Но у них есть свои несоответствия. Реестр представляет собой постоянно доступное место, доступное для процессора компьютерной системы. Они состоят из небольших воспоминаний быстрого хранения. Эта небольшая память используется, когда компьютер загружает данные из большой памяти в регистры для выполнения арифметических операций.
• Есть причина, по которой люди, не обращающие внимания на кеш, знают о кеше; то есть из-за иерархии кэш-памяти, которая проверяется с помощью модели без учета кеша.
• Принцип, объединяющий их все, заключается в разработке алгоритмов внешней памяти без знания размера кеша и блоков в кеше.

Предположение о высоком тайнике

Идеальная модель кеша — это предположение, которое имеет допущение, называемое «длинный кеш» , которое используется для расчета сложности кеша алгоритма. Это утверждение имеет математическое уравнение:

Z = Ω(B²) 

Here, 
Z is the size of the cache.
B is the size of the cache line.
Ω symbol is used to represent the lower bound of the algorithm or data. And that is the top speed any algorithm can get to.

Примеры алгоритма Cache-Oblivious

1. Разворот массива:

• Обращение массива — это обращение элементов в массиве без дополнительного хранения. Алгоритм обращения массива Бентли строит два параллельных сканирования с обеих сторон, каждое с противоположных концов массива. При каждом сканировании или шаге два элемента обмениваются своими позициями друг с другом.

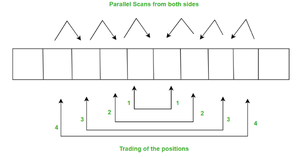
• Преимущества:
  • Алгоритм без кэширования использует то же количество операций чтения памяти, что и одно сканирование.
  • Алгоритм помогает реализовать обход N элементов, сканируя элементы один за другим в том порядке, в котором они хранятся.
• Ограничение:
  • Алгоритмы работают хуже, чем алгоритмы на основе ОЗУ и кэш-памяти, когда данные хранятся в основной памяти.

2. Транспонирование матрицы:

• Матричное транспонирование определяется следующим образом. Имея матрицу размера m × n, хранящуюся в построчном макете, мы должны вычислить и сохранить A ^T (A Transpose) в матрицу n × m B, которая также хранится в построчном макете.
  • Прямой алгоритм перестановки, использующий дважды вложенные циклы, приводит к Θ(mn) промахов кэша в одной из матриц. Причина промахов кеша в том, что увеличивается размер матрицы.
  • Кэш-промах происходит в результате загрузки одного блока из основной памяти в кеш.
  • Однако оптимальная сложность работы и кеша может быть достигнута с помощью стратегии «разделяй и властвуй».
    

    If n >= m, 
    we partition
    A = (A_1, A₂), 
    B = (B_1, B₂)

  • Затем несколько раз выполните ТРАНСП (A1, B1) и ТРАНСП (A2, B2). Точно так же, если m > n, мы делим матрицу A по горизонтали и матрицу B по вертикали и аналогичным образом выполняем два перестановки повторно.
• Преимущества:
  • Итеративный алгоритм перестановки матриц вызывает Ω(n ² ) промахов кэша для матрицы xn, когда матрица хранится в порядке строк или столбцов, что имеет коэффициент Θ(B), который, очевидно, имеет больше промахов кэша, чем кэш-память. оптимальный алгоритм.
• Ограничение:
  • Несмотря на то, что эти алгоритмы оптимальны в модели оперативной памяти и не обращают внимания на кеш, они не являются асимптотически оптимальными в отношении промахов кеша.

3. Бинарное дерево поиска (алгоритм «разделяй и властвуй»):

• Алгоритм «разделяй и властвуй» рекурсивно определяет размер проблемы. Позже данные помещаются в кеш (M), и в конечном итоге данные помещаются в один блок или строку кеша. Процесс анализа учитывает точную минуту, когда данные помещаются в кеш и помещаются в строку кеша. И, что удивительно, в этих случаях количество передач памяти меньше.
  • Хорошим примером алгоритма «разделяй и властвуй» является двоичное дерево.
  • В бинарном дереве каждое дерево имеет поддерево, левое или правое, т. е. каждый узел рекурсивного дерева имеет только одну ветвь, наиболее известную как вырожденная форма разделяй и властвуй.
  • В этом сценарии стоимость каждого листа уравновешивается стоимостью корневого узла, что оставляет нам одинаковый уровень рекурсии на каждом узле.
• Преимущества:
  • Согласно плану Ван Эмде Боаса, бинарное дерево поиска с узлами, помеченными определенными позициями, требует меньшего количества уровней рекурсии.
• Ограничение:
  • Структура данных, игнорирующая кеш, атрибутируется набором Бендерса, который использует двоичное дерево в качестве индексной структуры данных для эффективного поиска элемента-преемника для заданного значения. Он оказался худшим как по времени выполнения, так и по использованию памяти.

4. Сортировка слиянием:

• Позиционирование данных в определенном порядке часто называют сортировкой. В алгоритмах внешней памяти сортировка показывает как нижнюю, так и верхнюю границу. В своей статье Аггарвал и Виттер доказали способ сортировки количества передач памяти в модели сравнения, т.е.
  

  Θ( N /B [log_M/B N/ B ])

• Сортировка слиянием (M/B) — это способ сортировки алгоритма внешней памяти для достижения границы Аггарвала и Виттера. Чтобы понять контекст без учета кеша, во-первых, нам нужно увидеть алгоритм внешней памяти. В процессе слияния каждый блок данных поддерживает первые B элементов каждого списка; когда блок свободен, в него загружается следующий блок из списка. Таким образом, для слияния требуется Θ(N/B) передач памяти для конструктивного сканирования памяти.
  

  The total no. of memory transfers for this kind of sorting algorithm would be: T(N) = M/B T(N/ M/B) + Θ(N/B)
  The recursion tree has Θ(N/B) leaves,for a leaf cost of Θ(N/B)
  The number of levels in the recursion tree is log_M/B N, so the total cost is Θ(N/B log_{M/B N/B)}

• Дерево рекурсии — это не что иное, как бинарное дерево поиска.
• Теперь, в условиях отсутствия кеша, идеальным алгоритмом для использования является классическая двусторонняя сортировка слиянием, но тогда повторение становится
  

  T(N) = 2T(N/2) + Θ(N/B)

• Преимущества:
  • Кеширование забывающих методов позволяет использовать двустороннюю сортировку слиянием более эффективно, чем алгоритм внешней памяти.
  • Количество передач памяти для сортировки в модели сравнения равно Θ(N/B log _M/B N/B).
• Ограничение:
  • Сортировка слиянием поддерживает Ω((n/B) lg(n/Z)) промахов в кэше для входного размера n, что в Θ(lg Z) больше промахов в кэше, чем алгоритмы, оптимальные для кэша. Следовательно, сортировка слиянием сама по себе не является оптимальным алгоритмом кэширования.

использованная литература

• Кэшируйте забывающие алгоритмы и структуры данных. Эрик Д. Демейн (Лаборатория компьютерных наук Массачусетского технологического института)
• Анализ алгоритмов с учетом кеша
• Кэш-сознательное программирование в области компьютерных наук. DOI: 10.1145/384266.299772.
• Оценка структуры данных, не обращающей внимания на кэш Макс Вервер
• Кэш-забывчивые алгоритмы Харальда Прокопа