GRE Geometry | Круги
Круг - это двухмерная фигура. Это замкнутая фигура, в которой граница равноудалена от центра, а расстояние от центра до границы называется радиусом, и оно остается неизменным на протяжении всей фигуры.

C - центр круга. Периметр круга называется окружностью.
Важные свойства круга:
- Площадь круга = π * r * r
- Периметр круга = 2 * π * r
или π * диаметр - диаметр = 2 * радиус
Полукруг: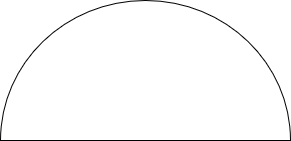
Важные свойства круга:
- Площадь полукруга = π * r * r / 2
- Периметр полукруга = * π * r
или π * диаметр / 2
π - отношение длины окружности к диаметру круга, которое одинаково для всей окружности, или,
= окружность / диаметр = π или окружность / (2 * радиус) = π
π - неповторяющееся и не завершающееся число, равное 22/7 или приблизительно 3,14.
Аккорд:
Это отрезок прямой, соединяющий две точки на окружности. Диаметр - это особый вид хорды, проходящей через центр окружности.
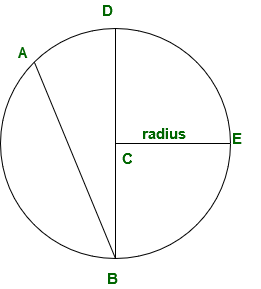
AB и BD - хорда данной окружности.
Дуга:
Рассмотрим любые две точки на окружности круга, длина между этими двумя точками, включая все точки между ними, называется дугой. Обычно дуга содержит 3 точки, чтобы избежать неоднозначности.
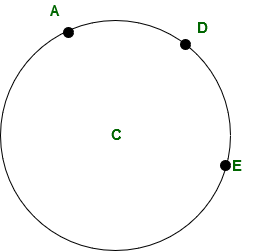
ADE - это дуга данного круга. D - это точка между A и E, чтобы избежать двусмысленности.
Как найти длину дуги?
Длина дуги = (угол, ограниченный дугой в центре / 360 °) * окружность
Что такое сектор?
Сектор - это область, покрытая дугой.
Площадь сектора = радиус * угол между секторами.
∠ ACED = 120 °
Площадь сектора = радиус * угол между секторами.
Касательная и точка касания:
Касательная - это отрезок прямой, который лежит на той же плоскости, что и окружность, и касается окружности только в одной точке. Эта точка называется точкой касания.
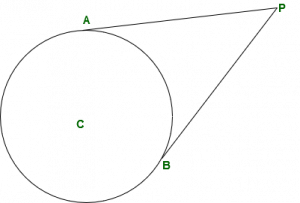
AP и BP касаются окружности, где A и B - точки касания. Радиус проведен до точки касания перпендикулярно касательной.
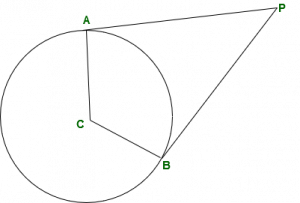
Касательные, проведенные из одной точки, равны по длине.
или AP = BP.
Что такое начертанная фигура и описанная фигура?
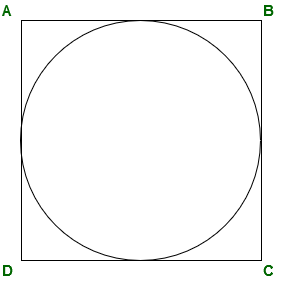
Вписанная фигура: когда круг покрывает все точки многоугольника, тогда многоугольник вписывается в круг.
Описанная фигура: когда круг находится внутри многоугольника, его периметр касается всех сторон многоугольника и каждая сторона многоугольника касается круга, тогда фигура называется описанной.
Что такое концентрические круги?
Два или более одинаковых круга разного радиуса являются концентрическими кругами.

Пример-1:
Каков радиус круга площадью 154 см 2 ?
Решение:
Площадь круга = π * радиус * радиус 154 = 22/7 * радиус * радиус (возьмем π = 22/7) 49 = радиус * радиус радиус = 7 см
Пример-2: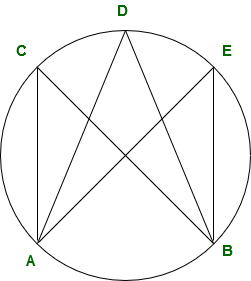
Если ∠ ADB = 65 °, то какова сумма ∠ ADB, ∠ ACB и ∠ AEB?
Решение:
Углы, образованные двумя точками в одной дуге, равны.
∠ ADB = ∠ ACB = ∠ AEB = 65 ° ∠ ADB + ∠ ACB + ∠ AEB = 195 °
Пример-3:
Каким будет периметр четырехугольника APBC, если радиус окружности 5 см, а длина CP равна 13?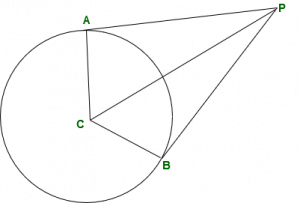
Решение:
Угол касательной в точке касания вместе с радиусом всегда составляет 90 °.
Итак, треугольник APC - это прямоугольный треугольник.
Примените теорему Пифагора в треугольнике APC:
AP 2 + AC 2 = ПК 2 AP 2 = ПК 2 - AC 2 AP 2 = 13 2 - 5 2 AP 2 = 169 - 25 AP 2 = 144 AP = 12
Поскольку касательные от одной и той же внешней точки равны по длине.
AP = BP = 12 см Периметр четырехугольника: = 12 + 12 + 5 + 5 = 34 см