Эффективность упаковки элементарной ячейки
Кристаллическая решетка состоит из относительно большого числа элементарных ячеек, каждая из которых содержит по одной составляющей частицы в каждой точке решетки. Трехмерную структуру с одним или несколькими атомами можно рассматривать как элементарную ячейку. Независимо от способа упаковки в элементарной ячейке всегда есть пустые места. Доля упаковки элементарной ячейки — это процент пустых пространств в элементарной ячейке, заполненных частицами. В этой статье мы узнаем об эффективности упаковки.
Эффективность упаковки
Эффективность упаковки — это доля общего объема твердого тела, занятая сферическими атомами.
Эффективность упаковки — это доля общего объема элементарной ячейки, занятая атомами, ионами или молекулами, составляющими решетку. Это вся площадь, которую каждая из этих частиц занимает в трех измерениях. Его можно понимать просто как определенный процент от общего объема твердого тела, который населен сферическими атомами.
Подобно координационному числу, величина эффективности упаковки указывает, насколько плотно упакованы частицы.
Формула эффективности упаковки
Формула эффективной упаковки такова:
Packing efficiency = (Volume occupied by particles in unit cell / Total volume of unit cell) × 100
Факторы, определяющие эффективность упаковки
Следующие элементы влияют на эффективность упаковки элементарной ячейки:
- Количество атомов в структуре решетки
- Объем элементарной ячейки
- Объем атомов
Эффективность упаковки можно оценить с помощью трех различных структур геометрии, а именно:
- Простая кубическая решетка
- Объемно-центрированная кубическая решетка
- Гранецентрированная кубическая решетка (или CCP или HCP Lattice)
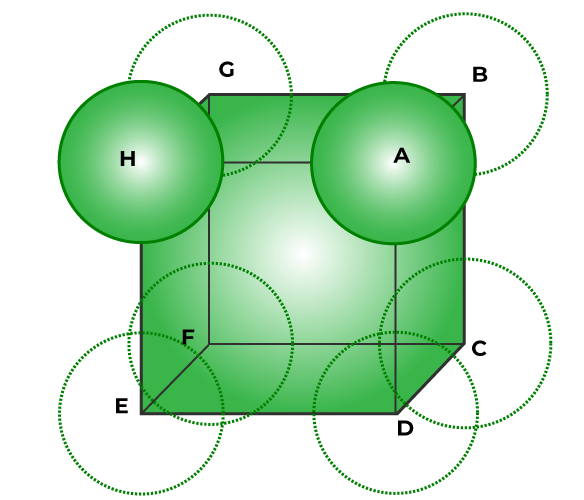
Эффективность упаковки металлического кристалла в простой кубической решетке
Следующие шаги используются для достижения эффективности упаковки металлического кристалла простой кубической решетки:
Step 1: Radius of sphere
In a simple cubic unit cell, spheres or particles are at the corners and touch along the edge. Below is an diagram of the face of a simple cubic unit cell.
It is evident that,
a=2r or r = a/2 …(Equation 1)
Where, r is the radius of atom and a is the length of unit cell edge.
Step 2: Volume of sphere:
Volume of a sphere = (4/3π)(r3)
Substitution for r from equation 1 gives,
∴ Volume of one particle = (4/3π)(a/2)3
∴ Volume of one particle = πa3 / 6 …(Equation 2)
Step 3: Total volume of particles:
Simple cubic unit cells only contain one particle.
∴ Volume occupied by particle in unit cell = πa3 / 6
Step 4: Packing Efficiency:
We have,
Packing efficiency = (Volume occupied by particles in unit cell / Total volume of unit cell) × 100
∴ Packing efficiency = ((πa3 / 6) / a3) × 100
∴ Packing efficiency = 100π / 6
∴ Packing efficiency = (100 × 3.142) / 6
∴ Packing efficiency = 52.36 %
Следовательно, в простой кубической решетке частицы занимают 52,36 % пространства, тогда как объем пустот, или оставшиеся 47,64 %, составляет пустое пространство.
Эффективность упаковки металлического кристалла в объемно-центрированной кубической решетке
Описанные ниже шаги используются для достижения эффективности упаковки металлического кристалла в объемно-центрированной кубической решетке.
Step 1: Radius of sphere:
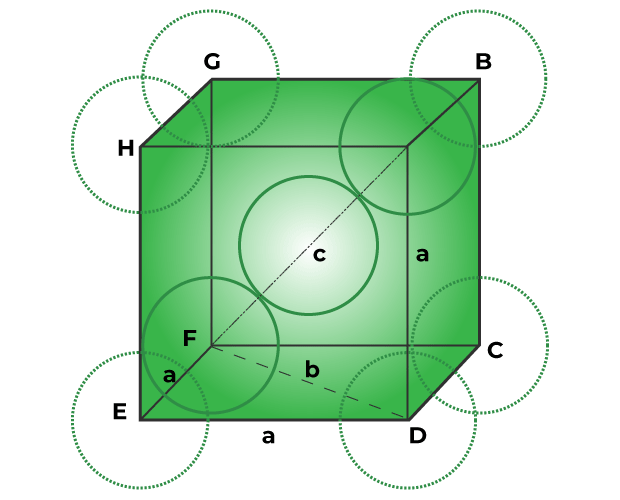
The corners of the bcc unit cell are filled with particles, and one particle also sits in the cube’s middle. The cube’s center particle hits two corner particles along its diagonal, as seen in the figure below.
The Pythagorean theorem is used to determine the particle’s (sphere’s) radius.
In triangle EFD,
b2 = a2 + a2
∴ b2 = 2a2
∴ b = √2 a
According to the Pythagoras theorem, now in triangle AFD,
c2 = a2 + b2
∴ c2 = a2 + 2a2
∴ c2 = 3a2
∴ c = √3 a
We can rewrite the equation as since the radius of each sphere equals r.
c = 4r
√3 a = 4r
∴ r = √3/4 a …(Equation 1)
Step 2: Volume of sphere:
Volume of sphere particle = 4/3 πr3. Substitution for r from equation 1, we get
∴ Volume of one particle = 4/3 π(√3/4 a)3
∴ Volume of one particle = 4/3 π × (√3)3/64 × a3
∴ Volume of one particle = √3 πa3 / 16
Step 3: Total volume of particles:
Unit cell bcc contains 2 particles. Hence,
volume occupied by particles in bcc unit cell = 2 × ((2√3 πa3) / 16)
∴ volume occupied by particles in bcc unit cell = √3 πa3 / 8 …(Equation 2)
Step 4: Packing Efficiency:
We have,
Packing efficiency = (Volume occupied by particles in unit cell / Total volume of unit cell) × 100
∴ Packing efficiency = (√3 πa3 / 8a3) × 100
∴ Packing efficiency = 68 %
В результате атомы занимают 68 % объема ОЦК элементарной решетки, а пустое пространство, или 32 %, остается незанятым.
Эффективность упаковки металлического кристалла в гранецентрированной кубической решетке
Следующие шаги используются для достижения эффективности упаковки металлического кристалла в гранецентрированной кубической решетке:
Step 1: Radius of sphere
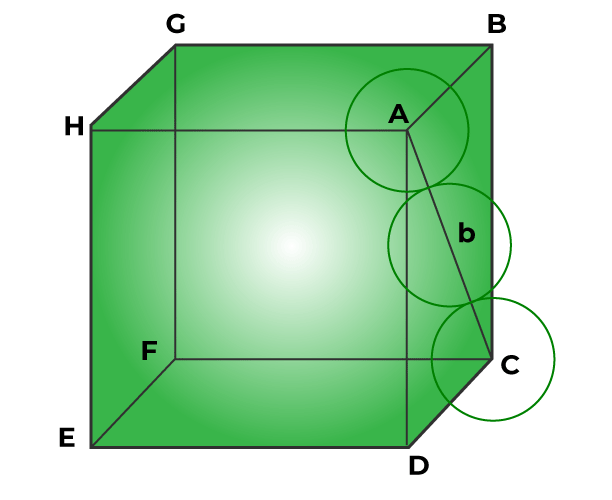
The corner particles are expected to touch the face ABCD’s central particle, as indicated in the figure below.
According to Pythagoras Theorem, the triangle ABC has a right angle.
AC2 = AB2 + BC2
∴ AC2 = a2 + a2
∴ AC2 = 2a2
∴ AC = √2 a …(Equation 1)
We can rewrite the equation as since the radius of each sphere equals r.
AC = 4r …(Equation 2)
From equation 1 and 2, we get
√2 a = 4r
∴ r = a / 2√2 …(Equation 3)
Step 2: Volume of sphere:
Volume of sphere particle = 4/3 πr3. Substitution for r from equation 3, we get
∴ Volume of one particle = 4/3 π(a / 2√2)3
∴ Volume of one particle = 4/3 πa3 × (1/2√2)3
∴ Volume of one particle = πa3 / 12√2
Step 3: Total volume of particles:
Unit cell bcc contains 4 particles. Hence,
volume occupied by particles in FCC unit cell = 4 × πa3 / 12√2
∴ volume occupied by particles in FCC unit cell = πa3 / 3√2
Step 4: Packing Efficiency:
We have,
Packing efficiency = (Volume occupied by particles in unit cell / Total volume of unit cell) × 100
∴ Packing efficiency = πa3 / 3√2 a3 × 100
∴ Packing efficiency = 74 %
В результате в кристаллической решетке ГЦК, ГПУ и ГПУ частицы занимают 74 % всего объема, а объем пустот, или пустое пространство, составляет 26 % всего объема.
Важность эффективной упаковки
Эффективность упаковки важна, так как:
- Прочная конструкция объекта проявляется в эффективности упаковки.
- Он демонстрирует различные твердые свойства, включая изотропию, консистенцию и плотность.
- Многочисленные характеристики твердых структур могут быть получены с помощью эффективности упаковки.
В следующей таблице указана эффективность упаковки нескольких твердотельных архитектур.
| Ячейка | Связь между а и г | Количество атомов в элементарной ячейке | Координационное число атомов | Эффективность упаковки | Свободное место |
|---|---|---|---|---|---|
| ССС | 0,5000а | 1 | 6 | 52,4% | 47,6% |
| BCC | 0,4330а | 2 | 8 | 68% | 32% |
| ФКК | 0,3535а | 4 | 12 | 74% | 26% |
Решенные примеры эффективности упаковки
Пример 1: Рассчитайте общий объем частиц в ОЦК решетке.
Решение:
Unit cell bcc contains 2 particles. Hence,
volume occupied by particles in bcc unit cell = 2 × ((2√3 πa3) / 16)
∴ volume occupied by particles in bcc unit cell = √3 πa3 / 8
Пример 2: Расчет эффективности упаковки гранецентрированной кубической решетки.
Решение:
We have,
Packing efficiency = (Volume occupied by particles in unit cell / Total volume of unit cell) × 100
∴ Packing efficiency = πa3 / 3√2 a3 × 100
∴ Packing efficiency = 74 %
Пример 3: Расчет эффективности упаковки простой кубической решетки.
Решение:
We have,
Packing efficiency = (Volume occupied by particles in unit cell / Total volume of unit cell) × 100
∴ Packing efficiency = ((πa3 / 6) / a3) × 100
∴ Packing efficiency = 100π / 6
∴ Packing efficiency = (100 × 3.142) / 6
∴ Packing efficiency = 52.36 %
Пример 4: Рассчитать объем сферических частиц объемно-центрированной кубической решетки.
Решение:
Volume of sphere particle = 4/3 πr3. Substitution for r from r = √3/4 a, we get
∴ Volume of one particle = 4/3 π(√3/4 a)3
∴ Volume of one particle = 4/3 π × (√3)3/64 × a3
∴ Volume of one particle = √3 πa3 / 16
Часто задаваемые вопросы об эффективности упаковки
Вопрос 1: Что такое гранецентрированная элементарная ячейка?
Ответ :
In a face centered unit cell the corner atoms are shared by 8 unit cells. Additionally, it has a single atom in the middle of each face of the cubic lattice. Two unit cells share these atoms in the faces of the molecules.
Вопрос 2: Какую роль играет эффективность упаковки?
Ответ :
Roles of Packing efficiency:
- The structure of the solid can be identified and determined using packing efficiency.
- Consistency, density, and isotropy are some of the effects. How well an element is bound can be learned from packing efficiency.
- Chemical, physical, and mechanical qualities, as well as a number of other attributes, are revealed by packing efficiency.
Вопрос 3: Насколько эффективны SCC, BCC и FCC при упаковке?
Отвечать:
The packing efficiency of different solid structures is as follows.
- Simple Cubic (SCC) – 52.4%
- Body Centered (BCC) – 68%
- Face Centered (FCC) – 74%
Вопрос 4: Насколько эффективна упаковка?
Отвечать:
Packing efficiency is the proportion of a given packing’s total volume that its particles occupy. In the crystal lattice, the constituent particles, such as atoms, ions, or molecules, are tightly packed. They have two options for doing so: cubic close packing (CCP) and hexagonal close packing (HCP). The complete amount of space is not occupied in either of the scenarios, leaving a number of empty spaces or voids.
Вопрос 5: Каковы факторы эффективности упаковки?
Отвечать:
The following elements affect how efficiently a unit cell is packed:
- Number of atoms in the lattice structure
- Unit cell volume
- Atoms volume