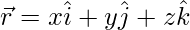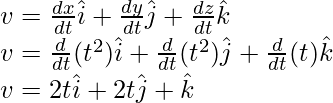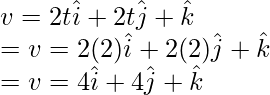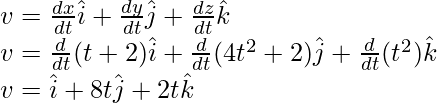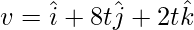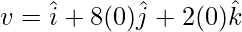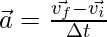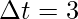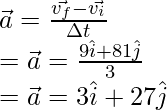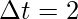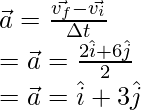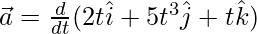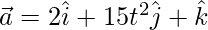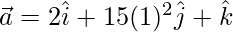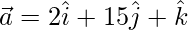Движение в трех измерениях

Частице, движущейся в одномерном пространстве, требуется только одна координата, чтобы задать ее положение. Точно так же в двух измерениях требуются две координаты. Трехмерные движения встречаются во многих местах реальной жизни, чтобы анализировать эти реальные ситуации. Нужно понимать движение и то, как математически обращаться с этими тремя координатами, чтобы описать траектории объектов, движущихся в трехмерной плоскости. Рассмотрим эти понятия подробно.

Движение в трехмерном пространстве

Предположим, что частица движется между двумя точками в трехмерном пространстве. Для описания положения этой частицы требуется вектор положения. Эти векторы всегда относятся к системе отсчета в начале координат. Следующие параметры необходимы для полного описания поведения частицы, движущейся в плоскости:

1. Должность
2. Скорость
3. Ускорение

Вектор положения

В трехмерном пространстве частица может находиться где угодно, ее нельзя описать одной координатой. В этом случае он обозначается относительно начала координат, а также определяет направление, в котором нужно двигаться, чтобы найти эту точку. Вот почему для описания положения требуется вектор. Вектор, который обозначает положение и направление положения частицы относительно начала координат, называется вектором положения. Вектор положения 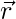для частицы дается,

Where x,  y, and z are their components along the x, y, and z-axis. 

Скорость

Скорость частицы, движущейся в трехмерном пространстве, можно описать двумя способами – средней скоростью и мгновенной скоростью. Когда частица ускоряется, она меняет свою скорость каждую секунду. Таким образом, скорости нельзя присвоить одно значение. В таких случаях предпочтительна мгновенная скорость , она описывает скорость и ее направление в конкретный момент времени. Это дается,

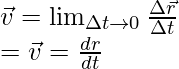
Скорость также может быть выражена как

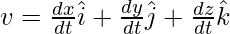
Средняя скорость – это отношение общего смещения к общему времени. Предположим, что частица выходит из 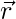к за общее время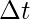

Скорость определяется выражением

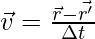
Ускорение

Ускорение тела, движущегося в плоскости, определяется скоростью изменения его скорости. Как и в случае со скоростью, здесь тоже может быть два случая – среднее ускорение и мгновенное ускорение. Среднее ускорение определяется отношением чистого изменения скорости объекта к общему затраченному времени. Обозначим начальную и конечную скорости через 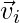а также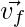

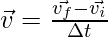
Мгновенное ускорение используется, когда ускорение тела изменяется во времени.

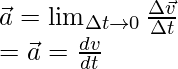
Разложив это на составляющие,

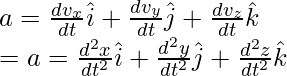
Величина ускорения также может быть рассчитана с использованием компонентов скорости,

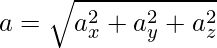
Относительное движение в трех измерениях

Относительное движение представляет собой скорость некоторого тела, наблюдаемого из одной системы отсчета. Эти понятия были известны в виде одномерных и двумерных пространств. Но эти понятия можно распространить и на трехмерные пространства. На рисунке ниже рассмотрим частицу P и системы отсчета S и S'. Положение системы отсчета S', измеренное в S, равно r _S'S , положение частицы P, измеренное относительно системы отсчета S', определяется как r _PS', а положение частицы P относительно системы отсчета S определяется как r _PS,

Обратите внимание на рисунок, что,

r _PS = r _PS' + r _S'S

Эти векторы также дают нам формулу для относительных скоростей, дифференцирующую приведенное выше уравнение,

⇒

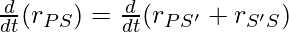
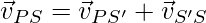
Интуитивно говоря, скорость частицы относительно S равна скорости S 'относительно S плюс скорость частицы относительно S. Снова дифференцируя это уравнение, уравнение для ускорения определяется как

⇒

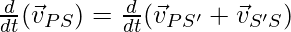
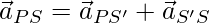
Ускорение частицы относительно S равно ускорению S' относительно S плюс ускорение частицы относительно S.

Примеры проблем

Вопрос 1: Найдите скорость в момент времени t = 2 частицы, движущейся по плоскости и положение которой задано: r = t ² i + t ² j + tk

Отвечать:

Given: the initial and final position vectors, 

r = t²i + t²j + tk

The velocity in this case is given by the formula, 

Here x(t) = t² and y(t) = t² and z(t) = t

Plugging these values into the equation, 

 At t = 2, 

Вопрос 2: Найдите скорость в момент t = 0 для частицы, которая движется в плоскости и положение которой задано, r = (t+2)i + (4t ² +2)j + t ² k

Отвечать:

Given: the initial and final position vectors, 

r =  (t+2)i + (4t²+2)j + t²k

The velocity in this case is given by the formula, 

Here x(t) = (t + 2) and y(t) = 4t² + 2and z(t) = t²

Plugging these values into the equation, 

At t = 0, 

⇒

⇒ v = i 

Вопрос 3: Найдите среднее ускорение между t = 0 и t = 3 для частицы, которая движется по плоскости и положение которой задано, v = 3ti + 3t ³ j + k

Отвечать:

Given: velocity as a function of time. 

v = 3ti + 3t³j + k

The velocity vector changes with time. The average acceleration is given by the formula, 

At t = 0 

v_i = 0i + 0j  + k 

At t = 3 

v_f = 9i + 81j  + k

Plugging the values into the above equation, 

Вопрос 4: Найдите среднее ускорение между t = 0 и t = 2 для частицы, которая движется по плоскости и положение которой задано, v = ti + 3tj + 2k

Отвечать:

Given: velocity as a function of time. 

v = ti + 3tj + 2k

The velocity vector changes with time. The average acceleration is given by the formula, 

At t = 0 

v_i = 0i + 0j  + 2k 

At t = 2 

v_f = 2i + 6j  + 2k

Plugging the values into the above equation, 

Вопрос 5. Найдите мгновенное ускорение в момент времени t = 1 частицы, движущейся по плоскости и положение которой задано, v = 2ti + 5t ³ j + tk.

Отвечать:

Given: velocity as a function of time. 

v = 2ti + 5t³j + tk

The velocity vector changes with time. The instantaneous acceleration is given by the formula, 

⇒ 

at t = 1, 

⇒ 

⇒