Доказательство того, что проблема коммивояжера - это NP Hard

Предварительные требования: Задача коммивояжера, NP Hard

Учитывая набор городов и расстояние между каждой парой городов, задача коммивояжера находит путь между этими городами, так что это кратчайший путь, и проходит через каждый город один раз, возвращаясь в исходную точку.

Проблема. Для графа G (V, E) проблема состоит в том, чтобы определить, имеет ли граф TSP, состоящий из стоимости не более K.
Объяснение -
Чтобы доказать NP-сложность задачи коммивояжера, нам нужно свести известную NP-сложную задачу к этой задаче. Мы проведем редукцию от задачи о гамильтоновом цикле к задаче коммивояжера.
Каждый пример задачи гамильтонова цикла состоит из графа G = (V, E), поскольку входные данные могут быть преобразованы в задачу коммивояжера, состоящую из графа G '= (V', E ') и максимальной стоимости K. Мы построит граф G 'следующим образом:
Для всех ребер e, принадлежащих E, добавьте стоимость ребра c (e) = 1. Соедините оставшиеся ребра e ', принадлежащие E', которых нет в исходном графе G , каждое со стоимостью c (e ') = 2.
И, установите .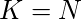
Новый граф G 'может быть построен за полиномиальное время, просто преобразовав G в полный граф G' и добавив соответствующие затраты. Это сокращение может быть доказано следующими двумя утверждениями:

• Предположим, что граф G содержит гамильтонов цикл, проходящий по всем вершинам V графа. Теперь эти вершины образуют ЗК с 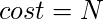Поскольку он использует все ребра исходного графа со стоимостью c (e) = 1. И, поскольку это цикл, он возвращается обратно в исходную вершину.
• Мы предполагаем, что граф G 'содержит ЗК со стоимостью, 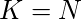. TSP проходит все вершины графа, возвращаясь к исходной вершине. Теперь, поскольку ни одна из вершин не исключена из графа и сумма затрат равна n, следовательно, он обязательно использует все ребра графа, присутствующие в E , со стоимостью 1, тем самым формируя гамильтонов цикл с графом G.

Таким образом, мы можем сказать, что граф G ' содержит ЗК, если граф G содержит гамильтонов цикл. Следовательно, любой пример задачи коммивояжера можно свести к примеру проблемы гамильтонова цикла. Таким образом, TSP NP-Hard.

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.