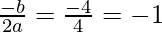Диапазон функции

Функции в математике можно рассматривать как торговые автоматы. Давая деньги в виде ввода, они дают какие-то банки или печенье взамен. Точно так же функции принимают некоторые входные числа и дают нам некоторые выходные данные. Можно сказать, что в реальной жизни Все можно сформулировать и решить с помощью функций. От проектирования зданий и архитектуры до мега-небоскребов, математическая модель почти всего в реальной жизни требует функций, поэтому нельзя избежать того, что функции имеют гигантское значение в нашей жизни. Домен и диапазон — это один аспект, посредством которого может быть описана функция.

Например: предположим, что на верхней части автомата написано, что для покупки чего-либо можно использовать только банкноты 20 и 50 рупий. Что, если кто-то использует купюры номиналом 10 рупий? Машина не даст никакого результата. Итак, домен представляет, какие входные данные мы можем иметь в функции. В этом случае банкноты 20 и 50 рупий являются доменом «торгового автомата». Точно так же, сколько бы денег человек ни положил в автомат, он никогда не получит из него бутербродов. Таким образом, здесь вступает в действие концепция диапазона, диапазон возможных результатов, которые может дать машина.

Диапазон и область определения функции

Домен функции:

Домен — это все значения, которые могут войти в функцию, для которых она дает действительный результат. Это набор всех возможных входов функции.

Например: На рисунке ниже f(x) = x ² . Набор всех входов называется доменом, а набор всех выходов считается диапазоном.

Как найти область определения функции?

Область определения функции должна содержать все действительные числа, кроме точек, где знаменатель становится равным нулю, а члены под квадратными корнями становятся отрицательными. Чтобы найти домен, попробуйте найти точки или входные значения, для которых функция не определена.

Вопрос 1: Найдите домен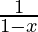

Отвечать:

This function can give undefined output when x = 1. So, then domain is R – {1}. 

Вопрос 2: Найдите домен следующей функции:

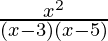
Ответ :

It is Important to not make the function either Infinity or Undefined, therefore, we need to see what Domain values can make the Function Undefined or Infinity.

Taking a look at the denominator, It is clear that the values 3 and 5 are making the denominator 0, hence, making the function Infinite which is not desirable. 

Therefore, the values x=3 and x=5 can’t be placed here.

The Domain will be R – {3,5}.

Вопрос 3: Найдите значения домена, для которых функции Y = (2x ² -1) и Z = (1-3x) равны.

Ответ :

Equating the two Functions:

2 x²– 1 = 1 – 3 x

2x² + 3x – 2 = 0

2x² + 4x – x – 2 = 0

2x (x + 2) – 1 (x+2)= 0

(2x – 1) (x + 2) = 0

x = 1/2, -2.

Therefore, the Domain values are {1/2, -2}.

Диапазон функции

Диапазон функции — это набор всех ее возможных выходов.

Пример: Рассмотрим функцию ƒ: A⇢A, где A = {1,2,3,4}.

Элементы множества доменов называются прообразами, а элементы множества совместных доменов, отображаемые на прообразы, называются изображениями. Диапазон функции — это набор всех изображений элементов в области. В этом примере диапазон функции равен {2,3}.

Как найти диапазон функции?

Диапазон — это разброс значений вывода функции. Если мы сможем вычислить максимальное и минимальное значения функции, мы сможем получить представление о диапазоне функции.

Вопрос 1: Найдите диапазон. е (х) =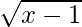

Отвечать:

Now, since the function is a square root, it can never give negative values as output. So, the minimum value can only be 0 at x = 1. Maximum value can go up to infinity as we keep on increasing x. 

So, the range of the function is [0,∞). 

Вопрос 2: Область определения функции ƒ, определяемой формулой f(x) = 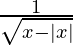является?

Отвечать:

Given, f(x) = . 

One has to ensure two things while selecting the set of domain, 

• Denominator never goes to zero.
• Term is inside the square root doesn’t become negative.

Let’s expand what’s written inside term within square root. 

 

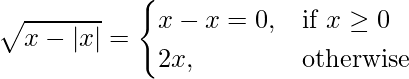
In this case, we cannot put either of the values, x ≥ 0 or x < 0. 

Hence, f is not defined for any x ∈ R. So, the domain is an empty set. 

Область определения и область значений квадратичных функций

Квадратичные функции — это функции вида f(x) = ax ² + bx + c, где a, b и c — константы, а a ≠ 0. График квадратичной функции имеет форму параболы. Это в основном изогнутая форма, открывающаяся вверх или вниз.

Давайте посмотрим, как построить график квадратичных функций,

Итак, в нашей квадратичной функции

• если a > 0, парабола открывается вверх.
• если a < 0, парабола открывается вниз.

Теперь вершина — это самая высокая или самая низкая точка нашей кривой в зависимости от графика квадратичной функции. Найти вершину графика общего квадратного выражения.

В стандартной квадратичной форме вершина определяется выражением 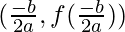Сначала нужно найти значение x вершины, а затем просто подключить его к функции, чтобы получить значение y.

Note: Each curve is symmetrical around its vertical axis. 

Давайте посмотрим на некоторые примеры,

Вопрос: Постройте график функции f(x) = 2x ² + 4x + 2.

Отвечать:

Comparing this equation with the general quadratic function equation. a = 2, b = -4 and c = 2. 

Since a > 0, this parabola will open upwards. 

• Vertex x-value = 
• Vertex y-value = 2(-1)² + 4(-1) + 2 = 0

So, the vertex is at (-1,0). Since the parabola opens upwards, this must be the minimum value of the function. 

The point where graph cuts y-axis is (0,2). 

Диапазон и область определения квадратичных функций можно легко узнать, построив график. Не всегда нужно строить полный график, для дальности нужно знать только направление параболы (вверх или вниз) и значение параболы в вершине. Значение в вершине всегда либо минимальное, либо максимальное, в зависимости от направления параболы. Областью определения таких функций всегда являются целые действительные числа, потому что они определены везде, т.е. нет значения ввода, которое могло бы привести к тому, что они дали undefined в качестве вывода.

Давайте посмотрим на другой пример, касающийся домена и диапазона параболы.

Вопрос: Постройте график и найдите область определения и область значений данной функции, f(x) = -x ² + 4.

Отвечать:

Since, a = -1. Parabola will open downwards i.e; there will be no minimum value, it will extend to infinity. But there will be a maximum value which will occur at vertex. 

To find the position of the vertex, previous formula can be used. The vertex is at position (0,4). 

The value at vertex (0,4) = (0)² + 4 = 4. 

So, the maximum value is 4 and minimum value is negative of infinity. 

Range of the function – (-∞, 4] and the domain is R.