Дерево сегментов | Минимальный запрос диапазона
Мы представили дерево сегментов на простом примере в предыдущем посте. В этом посте проблема запроса минимального диапазона обсуждается как еще один пример, где можно использовать дерево сегментов. Постановка проблемы следующая:
У нас есть массив arr[0 . . . п-1]. Мы должны иметь возможность эффективно находить минимальное значение от индекса qs (начало запроса) до qe (конец запроса), где 0 <= qs <= qe <= n-1 .
Простое решение — запустить цикл от qs до qe и найти минимальный элемент в заданном диапазоне. Это решение занимает O (n) времени в худшем случае.
Другим решением является создание двумерного массива, в котором запись [i, j] хранит минимальное значение в диапазоне arr[i..j]. Минимум заданного диапазона теперь можно вычислить за время O(1), но предварительная обработка занимает время O(n^2). Кроме того, для этого подхода требуется дополнительное пространство O (n ^ 2), которое может стать огромным для больших входных массивов.
Дерево сегментов можно использовать для предварительной обработки и выполнения запросов за умеренное время. При использовании дерева сегментов время предварительной обработки составляет O(n), а временная сложность запроса минимального диапазона составляет O(Logn). Для хранения дерева сегментов требуется дополнительное пространство O(n).
Представление деревьев сегментов
1. Листовые узлы — это элементы входного массива.
2. Каждый внутренний узел представляет минимум всех листьев под ним.
Представление дерева в виде массива используется для представления деревьев сегментов. Для каждого узла с индексом i левый дочерний узел имеет индекс 2*i+1, правый дочерний узел имеет индекс 2*i+2, а родительский узел имеет индекс ⌊(i – 1) / 2⌋ .
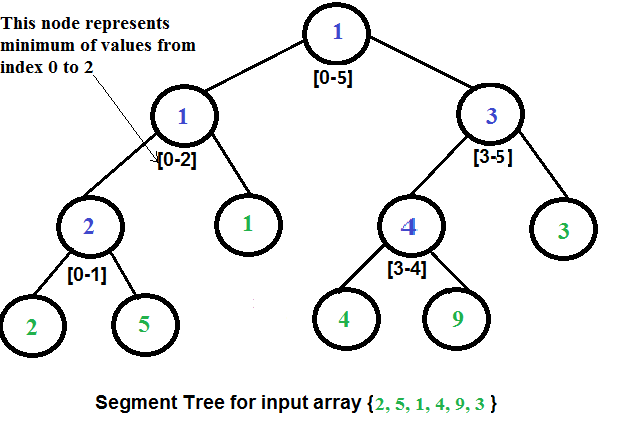
Построение дерева сегментов из заданного массива
Начнем с сегмента arr[0 . . . п-1]. и каждый раз делим текущий отрезок на две половины (если он еще не стал отрезком длины 1), а затем вызываем одну и ту же процедуру на обеих половинках, и для каждого такого отрезка сохраняем минимальное значение в дереве отрезков узел.
Все уровни построенного дерева отрезков будут полностью заполнены, кроме последнего уровня. Кроме того, дерево будет полным двоичным деревом, потому что мы всегда делим сегменты на две половины на каждом уровне. Поскольку построенное дерево всегда является полным бинарным деревом с n листьями, внутренних узлов будет n-1. Таким образом, общее количество узлов будет 2*n – 1.
Высота дерева сегментов будет ⌈log₂n⌉ . Так как дерево представлено в виде массива и должна поддерживаться связь между родительским и дочерним индексами, размер памяти, выделенной для дерева сегментов, будет 2 * 2 ⌈log 2 n⌉ – 1 .
Запрос минимального значения заданного диапазона
После того, как дерево построено, как выполнить запрос минимального диапазона, используя построенное дерево сегментов. Ниже приведен алгоритм получения минимума.
// qs --> query start index, qe --> query end index
int RMQ(node, qs, qe)
{
if range of node is within qs and qe
return value in node
else if range of node is completely outside qs and qe
return INFINITE
else
return min( RMQ(node"s left child, qs, qe), RMQ(node"s right child, qs, qe) )
}Реализация:
Выход:
Minimum of values in range [1, 5] is = 2
Сложность времени:
Временная сложность построения дерева составляет O(n). Всего узлов 2n-1, и значение каждого узла вычисляется только один раз при построении дерева.
Временная сложность запроса составляет O (Logn). Чтобы запросить минимум диапазона, мы обрабатываем не более двух узлов на каждом уровне, а количество уровней равно O (Logn).
Вспомогательное пространство : O(n), поскольку занято n дополнительных мест.
Пожалуйста, обратитесь к следующим ссылкам для получения дополнительных решений проблемы минимального запроса диапазона.
https://www.geeksforgeeks.org/range-minimum-query-for-static-array/
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Связанная тема: Дерево сегментов