Анализ алгоритма | Набор 5 (Введение в амортизированный анализ)

Амортизированный анализ используется для алгоритмов, в которых случайная операция выполняется очень медленно, но большинство других операций выполняется быстрее. В амортизированном анализе мы анализируем последовательность операций и гарантируем среднее время наихудшего случая, которое меньше, чем время наихудшего случая конкретной дорогостоящей операции.
Примеры структур данных, операции которых анализируются с помощью амортизированного анализа, - это хеш-таблицы, непересекающиеся множества и Splay Trees.

Рассмотрим пример простой вставки хеш-таблицы. Как мы определяем размер стола? Существует компромисс между пространством и временем: если мы увеличим размер хеш-таблицы, время поиска станет медленным, но требуемое пространство станет большим.

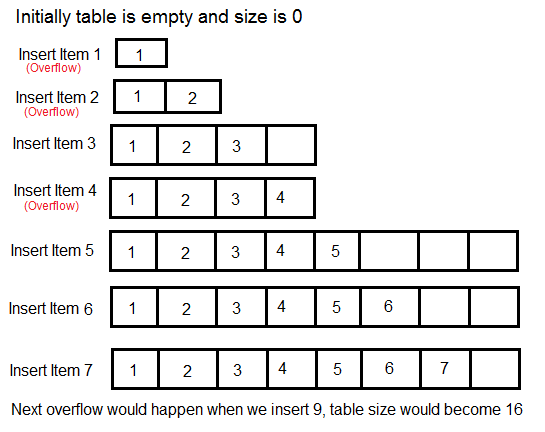
Решением этой проблемы компромисса является использование динамической таблицы (или массивов). Идея состоит в том, чтобы увеличивать размер таблицы всякий раз, когда она заполняется. Ниже приведены шаги, которые необходимо выполнить, когда стол заполнится.
1) Выделите память для таблицы большего размера, обычно вдвое больше старой таблицы.
2) Скопируйте содержимое старой таблицы в новую таблицу.
3) Освободите старый стол.

Если в таблице есть свободное место, мы просто вставляем новый элемент в доступное место.

Какова временная сложность n вставок по указанной выше схеме?
Если мы используем простой анализ, в худшем случае стоимость вставки составляет O (n). Следовательно, в худшем случае стоимость n вставок равна n * O (n), что составляет O (n ² ). Этот анализ дает верхнюю границу, но не точную верхнюю границу для n вставок, поскольку все вставки не занимают Θ (n) времени.

Таким образом, используя амортизированный анализ, мы смогли доказать, что схема динамической таблицы имеет время вставки O (1), что является отличным результатом для хеширования. Также концепция динамической таблицы используется в векторах в C ++, ArrayList в Java.

Ниже приведены несколько важных примечаний.
1) Амортизированная стоимость последовательности операций может рассматриваться как расходы наемного работника. Средние ежемесячные расходы человека меньше или равны зарплате, но человек может потратить больше денег в конкретный месяц, купив машину или что-то в этом роде. В другие месяцы он или она откладывают деньги на дорогой месяц.

2) Вышеупомянутый амортизированный анализ, выполненный для примера динамического массива, называется агрегатным методом . Есть еще два эффективных способа проведения амортизированного анализа, которые называются «Метод бухгалтерского учета». и потенциальный метод. Мы обсудим два других метода в отдельных сообщениях.

3) Амортизированный анализ не предполагает вероятности. Существует также другое понятие времени выполнения в среднем случае, когда алгоритмы используют рандомизацию, чтобы сделать их быстрее, а ожидаемое время выполнения быстрее, чем время выполнения в наихудшем случае. Эти алгоритмы анализируются с помощью рандомизированного анализа. Примерами этих алгоритмов являются рандомизированная быстрая сортировка, быстрый выбор и хеширование. Скоро мы расскажем о рандомизированном анализе в другом посте.

Амортизированный анализ вставки в красно-черное дерево

Давайте обсудим амортизированный анализ операций красно-черного дерева (вставка) с использованием потенциального метода.

Для проведения амортизированного анализа операции вставки красно-черного дерева мы используем потенциальный (или физический) метод. Для потенциального метода определим потенциальную функцию 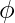который отображает структуру данных на неотрицательное действительное значение. Операция может привести к изменению этого потенциала.

Определим потенциальную функцию 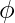следующим образом:

(1)

где n - узел красно-черного дерева

Возможная функция 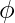знак равно , по всем узлам красно-черного дерева.

Далее мы определяем амортизированное время операции как:

Амортизированное время = c + (час)

(h) = (ч ') - (час)
где h и h '- состояния красно-черного дерева до и после операции соответственно.
c - фактическая стоимость операции

Изменение потенциала должно быть положительным для низкозатратных операций и отрицательным для высокозатратных операций.

Новый узел вставлен на лист красно-черного дерева. У нас есть листья красно-черного дерева любого из следующих типов:

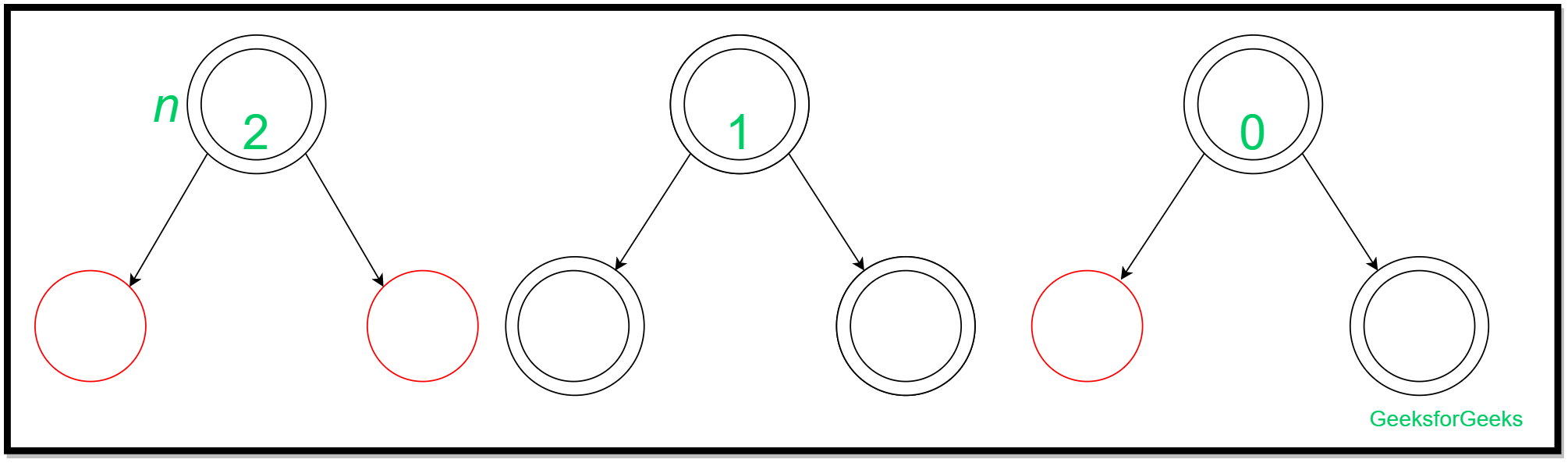
Вложения и их амортизированный анализ можно представить в виде:
(1)

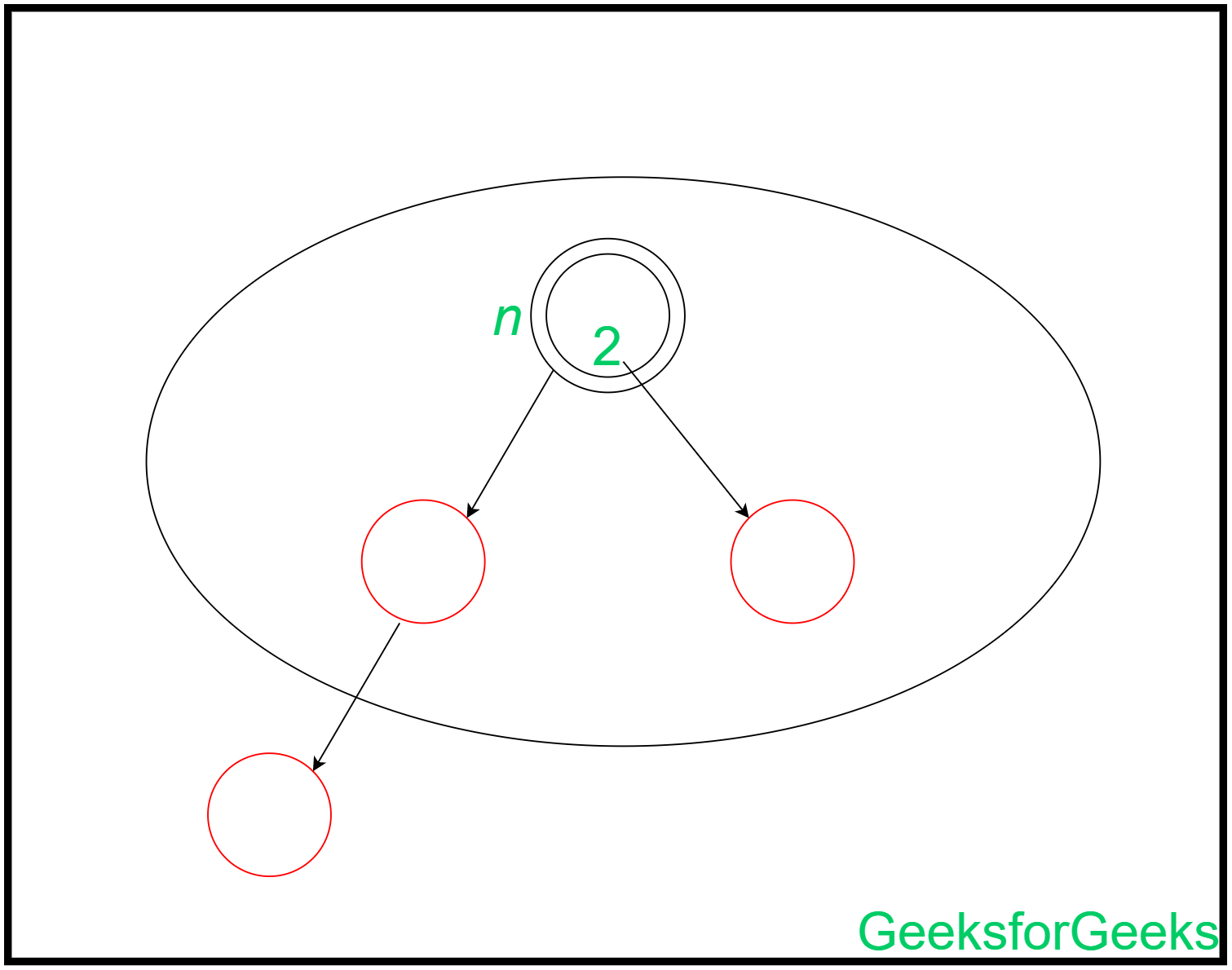
Эта вставка выполняется сначала перекрашиванием родительского элемента и другого брата (красный цвет). Затем прародитель и дядя этого листового узла рассматриваются для дальнейшей перекраски, что приводит к амортизированной стоимости, равной -1 (когда дедушка и бабушка листового узла красный), -2 (когда дядя листа черный, а дедушка и бабушка черные) или +1 (когда дядя листа красный, а дедушка или бабушка черные). Вставка может быть представлена как:

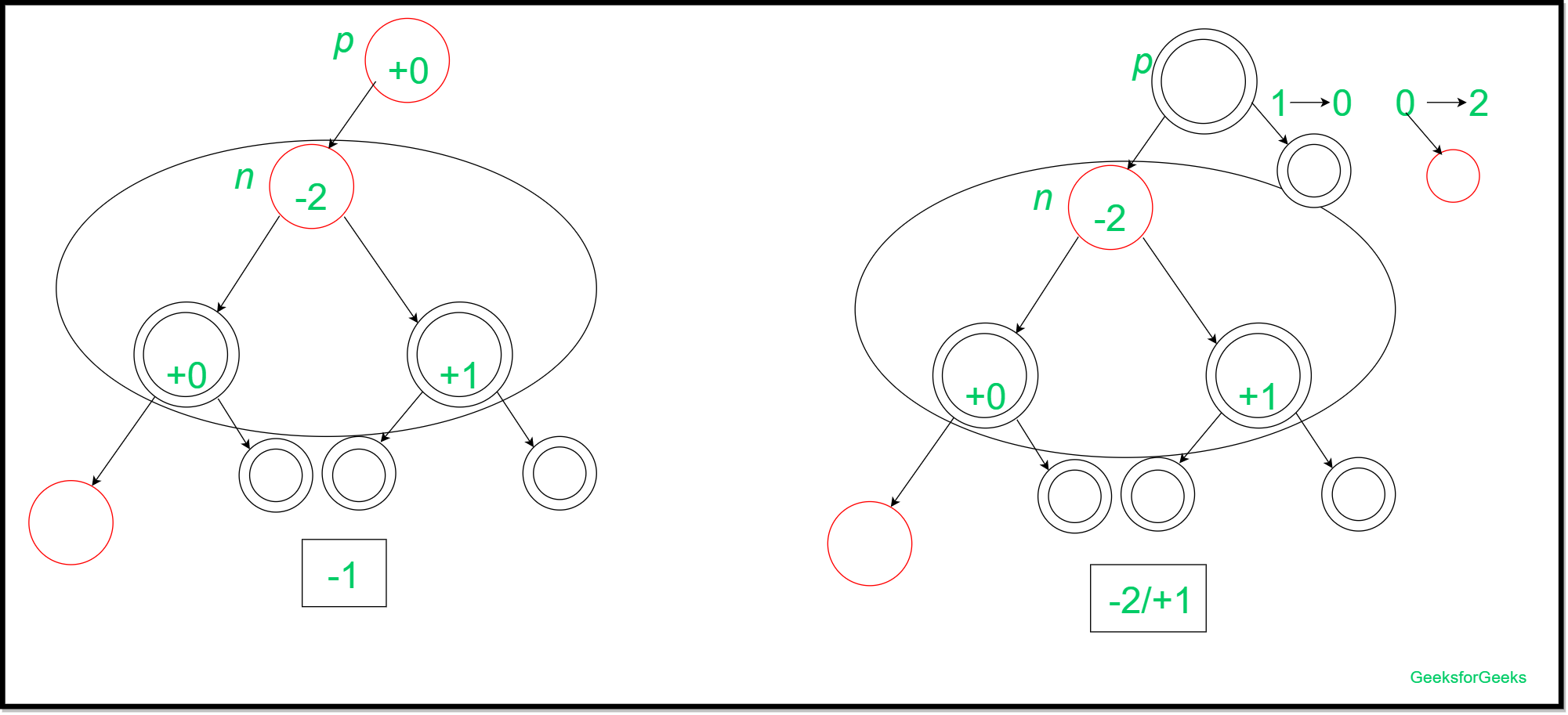
(2)

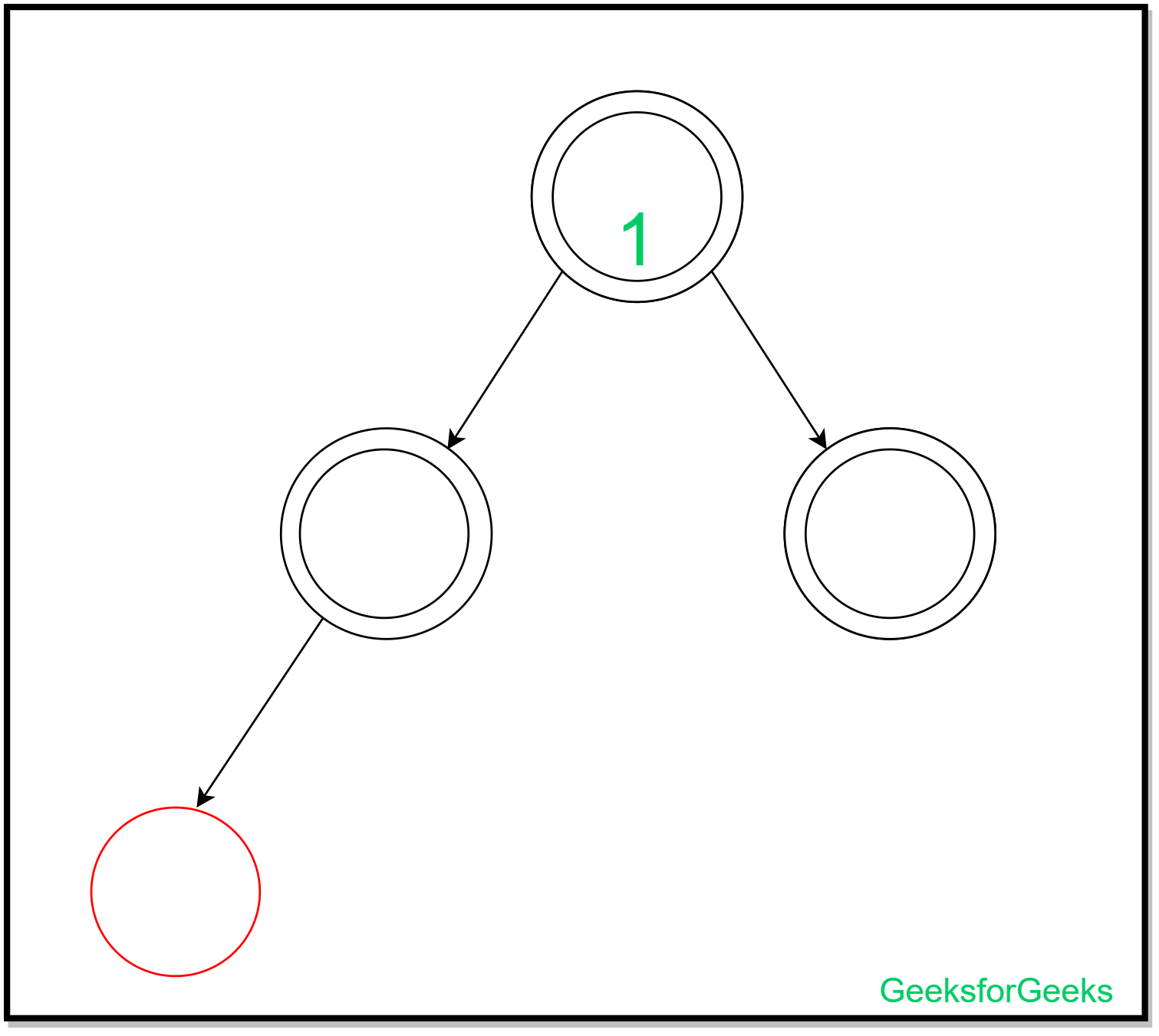
В этой вставке узел вставляется без каких-либо изменений, поскольку глубина черного листа остается неизменной. Это тот случай, когда у листа может быть черный брат или нет ни одного брата (поскольку мы считаем цвет цвета нулевого узла черным).

Итак, амортизированная стоимость этой вставки равна 0 .

(3)

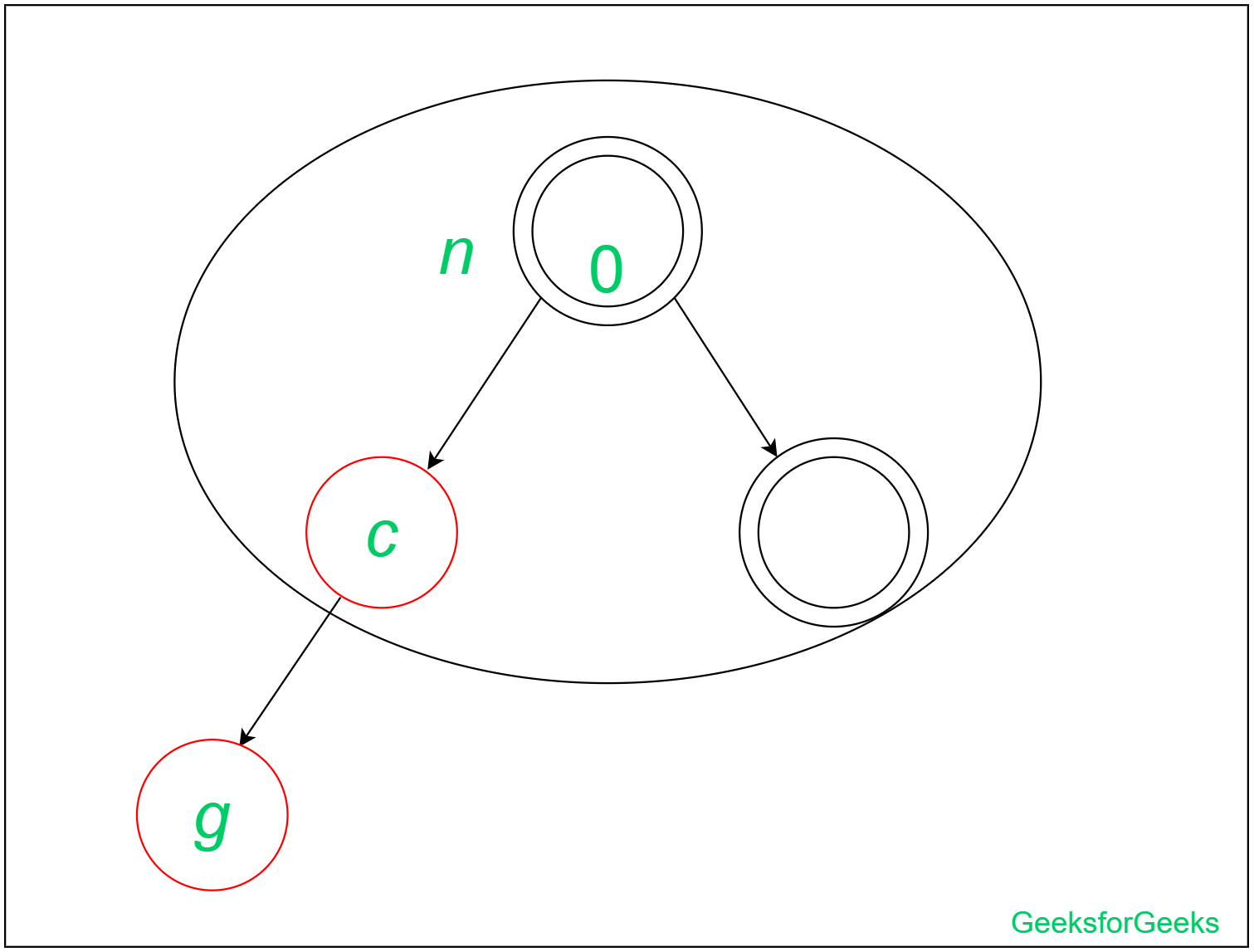
В этой вставке мы не можем перекрашивать листовой узел, его родителя и брата так, чтобы глубина черного оставалась такой же, как и раньше. Итак, нам нужно выполнить вращение влево-влево.

После поворота нет никаких изменений, если прародитель g (вставленный узел) черный. Кроме того, для случая Red Grandparent g (вставленный узел) у нас нет никаких изменений. Итак, вставка завершена с амортизированной стоимостью = +2 . Вставка изображена ниже:

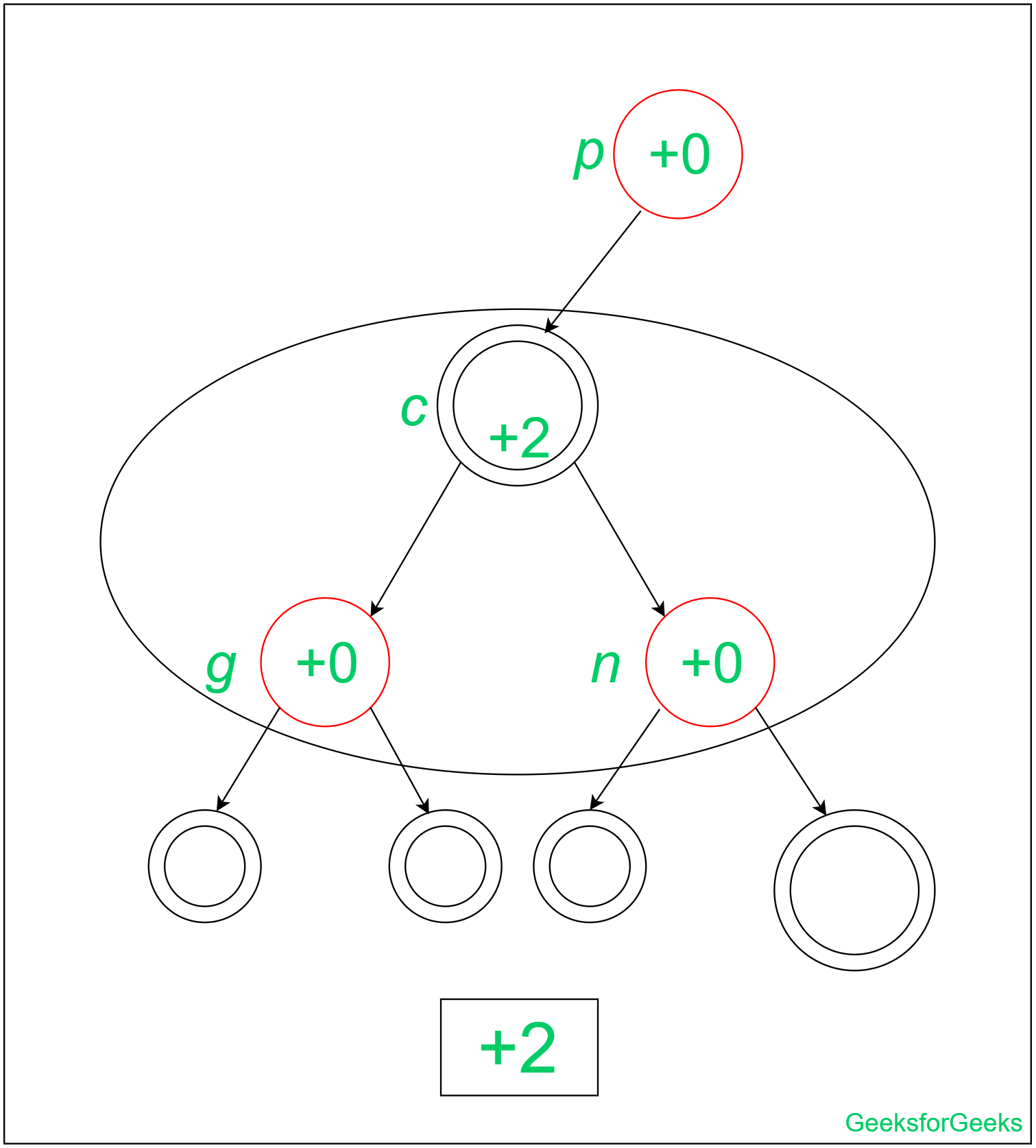
После расчета этих конкретных амортизированных затрат на листовой части красно-черного дерева мы можем обсудить природу общей амортизированной стоимости вставки в красно-черное дерево. Поскольку это может случиться, что два красных узла могут иметь отношения родитель-потомок до корня красно-черного дерева.

Таким образом, в крайнем (или угловом) случае мы уменьшаем количество черных узлов с двумя красными дочерними элементами на 1 и максимально увеличиваем количество черных узлов без красных дочерних элементов на 1, оставляя чистую потерю не более 1 для потенциального функция. Поскольку за каждую операцию платит одна единица потенциала, поэтому

(час) п
где n - общее количество узлов

Таким образом, общая амортизированная стоимость вставки в Красно-Черное дерево составляет O (n) .

Если у вас возникнут сомнения относительно вставок в красно-черное дерево, вы можете обратиться к Вставки в красно-черное дерево.

Источники:
Лекция в Беркли 35: Амортизированный анализ
Лекция 13 Массачусетского технологического института: Амортизированные алгоритмы, удвоение таблицы, потенциальный метод
http://www.cs.cornell.edu/courses/cs3110/2011sp/lectures/lec20-amortized/amortized.htm
http://web.iitd.ac.in/~csz188551/COL106_2019/

Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.