Алгоритм генерации линий Брезенхема

Опубликовано: 20 Января, 2022

Даны координаты двух точек A (x1, y1) и B (x2, y2). Задача найти все промежуточные точки, необходимые для рисования линии AB на экране пикселей компьютера. Обратите внимание, что каждый пиксель имеет целочисленные координаты.
Примеры:

 Ввод: A (0,0), B (4,4)
Выход: (0,0), (1,1), (2,2), (3,3), (4,4)

Ввод: A (0,0), B (4,2)
Выход: (0,0), (1,0), (2,1), (3,1), (4,2)

Ниже приведены некоторые предположения для упрощения алгоритма.

  1. Проводим линию слева направо.
  2. x1 <x2 и y1 <y2
  3. Наклон линии составляет от 0 до 1. Проводим линию снизу слева направо.

Давайте разберемся в этом процессе, рассмотрев сначала наивный путь.

 // Наивный способ рисования линии
void naiveDrawLine (x1, x2, y1, y2)
{
   т = (у2 - у1) / (х2 - х1)
   для (x = x1; x <= x2; x ++) 
   {    
      // Предполагая, что функция раунда находит
      // ближайшее целое число к заданному числу с плавающей запятой.
      y = круглый (mx + c);    
      печать (х, у); 
   }
}

Вышеупомянутый алгоритм работает, но он медленный. Идея алгоритма Брезенхема состоит в том, чтобы избежать умножения и сложения с плавающей запятой для вычисления mx + c, а затем вычисления округленного значения (mx + c) на каждом шаге. В алгоритме Брезенхема мы перемещаемся по оси x с единичными интервалами.

  1. Мы всегда увеличиваем x на 1 и выбираем следующий y, нужно ли нам перейти к y + 1 или остаться на y. Другими словами, из любой позиции (X k , Y k ) нам нужно выбирать между (X k + 1, Y k ) и (X k + 1, Y k + 1).

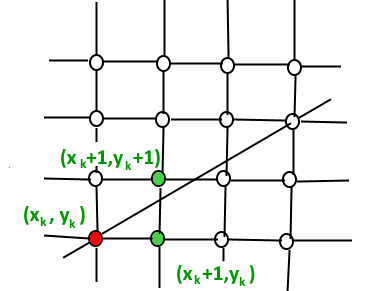
  1. Мы хотели бы выбрать значение y (среди Y k + 1 и Y k ), соответствующее точке, которая находится ближе к исходной линии.

Нам нужен параметр решения, чтобы решить, выбрать ли Y k + 1 или Y k в качестве следующей точки. Идея состоит в том, чтобы отслеживать ошибку наклона от предыдущего приращения до y. Если ошибка наклона становится больше 0,5, мы знаем, что линия переместилась вверх на один пиксель, и что мы должны увеличить нашу координату y и скорректировать ошибку, чтобы представить расстояние от вершины нового пикселя - что делается путем вычитания единицы. от ошибки.

 // Изменение наивного способа использования параметра
// решить следующий y .
void withDecisionParameter (x1, x2, y1, y2)
{
   т = (у2 - у1) / (х2 - х1)
   slope_error = [Некоторое начальное значение]
   для (x = x1, y = y1; x = 0,5)  
   {       
      y ++;       
      slope_error - = 1.0;    
   }
}

Как избежать арифметики с плавающей запятой
Вышеупомянутый алгоритм по-прежнему включает арифметику с плавающей запятой. Чтобы избежать арифметики с плавающей запятой, учитывайте значение ниже значения m.
т = (у2 - у1) / (х2 - х1)
Умножаем обе части на (x2 - x1)
Мы также меняем slope_error на slope_error * (x2 - x1). Чтобы избежать сравнения с 0.5, мы изменим его на slope_error * (x2 - x1) * 2.
Кроме того, обычно предпочтительнее сравнивать с 0, чем с 1.

 // Модификация вышеуказанного алгоритма, чтобы избежать плавающих
// точечная арифметика и сравнение с 0.
пустота брезенхема (x1, x2, y1, y2)
{
   m_new = 2 * (y2 - y1)
   slope_error_new = [Некоторое начальное значение]
   для (x = x1, y = y1; x = 0)  
   {       
      y ++;       
      slope_error_new - = 2 * (x2 - x1);    
   }
}

The initial value of slope_error_new is 2*(y2 – y1) – (x2 – x1). Refer this for proof of this value
Below is the implementation of above algorithm. 
 

C++

// C++ program for Bresenham’s Line Generation
// Assumptions :
// 1) Line is drawn from left to right.
// 2) x1 < x2 and y1 < y2
// 3) Slope of the line is between 0 and 1.
//    We draw a line from lower left to upper
//    right.
#include<bits/stdc++.h>
using namespace std;
 
// function for line generation
void bresenham(int x1, int y1, int x2, int y2)
{
   int m_new = 2 * (y2 - y1);
   int slope_error_new = m_new - (x2 - x1);
   for (int x = x1, y = y1; x <= x2; x++)
   {
      cout << "(" << x << "," << y << ") ";
 
      // Add slope to increment angle formed
      slope_error_new += m_new;
 
      // Slope error reached limit, time to
      // increment y and update slope error.
      if (slope_error_new >= 0)
      {
         y++;
         slope_error_new  -= 2 * (x2 - x1);
      }
   }
}
 
// driver function
int main()
{
  int x1 = 3, y1 = 2, x2 = 15, y2 = 5;
  bresenham(x1, y1, x2, y2);
  return 0;
}

Java

// Java program for Bresenhams Line Generation
// Assumptions :
// 1) Line is drawn from left to right.
// 2) x1 < x2 and y1 < y2
// 3) Slope of the line is between 0 and 1.
// We draw a line from lower left to upper
// right.
class GFG
{
    // function for line generation
    static void bresenham(int x1, int y1, int x2,
                                         int y2)
    {
        int m_new = 2 * (y2 - y1);
        int slope_error_new = m_new - (x2 - x1);
     
        for (int x = x1, y = y1; x <= x2; x++)
        {
            System.out.print("(" +x + "," + y + ") ");
 
            // Add slope to increment angle formed
            slope_error_new += m_new;
 
            // Slope error reached limit, time to
            // increment y and update slope error.
            if (slope_error_new >= 0)
            {
                y++;
                slope_error_new -= 2 * (x2 - x1);
            }
        }
    }        
 
    // Driver code
    public static void main (String[] args)
    {
        int x1 = 3, y1 = 2, x2 = 15, y2 = 5;   
        bresenham(x1, y1, x2, y2);
    }
}
 
// This code is contributed by Anant Agarwal.

Python3

# Python 3 program for Bresenham’s Line Generation
# Assumptions :
# 1) Line is drawn from left to right.
# 2) x1 < x2 and y1 < y2
# 3) Slope of the line is between 0 and 1.
# We draw a line from lower left to upper
# right.
 
 
# function for line generation
def bresenham(x1,y1,x2, y2):
 
    m_new = 2 * (y2 - y1)
    slope_error_new = m_new - (x2 - x1)
 
    y=y1
    for x in range(x1,x2+1):
     
        print("(",x ,",",y ,") ")
 
        # Add slope to increment angle formed
        slope_error_new =slope_error_new + m_new
 
        # Slope error reached limit, time to
        # increment y and update slope error.
        if (slope_error_new >= 0):
            y=y+1
            slope_error_new =slope_error_new - 2 * (x2 - x1)
         
     
 
 
# driver function
if __name__=="__main__":
    x1 = 3
    y1 = 2
    x2 = 15
    y2 = 5
    bresenham(x1, y1, x2, y2)
 
#This code is contributed by ash264

C#

// C# program for Bresenhams Line Generation
// Assumptions :
// 1) Line is drawn from left to right.
// 2) x1 < x2 and y1< y2
// 3) Slope of the line is between 0 and 1.
// We draw a line from lower left to upper
// right.
using System;
 
class GFG {
     
    // function for line generation
    static void bresenham(int x1, int y1, int x2,
                                        int y2)
    {
         
        int m_new = 2 * (y2 - y1);
        int slope_error_new = m_new - (x2 - x1);
     
        for (int x = x1, y = y1; x <= x2; x++)
        {
            Console.Write("(" + x + "," + y + ") ");
 
            // Add slope to increment angle formed
            slope_error_new += m_new;
 
            // Slope error reached limit, time to
            // increment y and update slope error.
            if (slope_error_new >= 0)
            {
                y++;
                slope_error_new -= 2 * (x2 - x1);
            }
        }
    }        
 
    // Driver code
    public static void Main ()
    {
        int x1 = 3, y1 = 2, x2 = 15, y2 = 5;
         
        bresenham(x1, y1, x2, y2);
    }
}
 
// This code is contributed by nitin mittal.

PHP

<?php
// PHP program for Bresenham’s
// Line Generation Assumptions :
 
// 1) Line is drawn from
// left to right.
// 2) x1 < x2 and y1 < y2
// 3) Slope of the line is
// between 0 and 1.
// We draw a line from lower
// left to upper right.
 
// function for line generation
function bresenham($x1, $y1, $x2, $y2)
{
$m_new = 2 * ($y2 - $y1);
$slope_error_new = $m_new - ($x2 - $x1);
for ($x = $x1, $y = $y1; $x <= $x2; $x++)
{
    echo "(" ,$x , "," , $y, ") ";
 
    // Add slope to increment
    // angle formed
    $slope_error_new += $m_new;
 
    // Slope error reached limit,
    // time to increment y and
    // update slope error.
    if ($slope_error_new >= 0)
    {
        $y++;
        $slope_error_new -= 2 * ($x2 - $x1);
    }
}
}
 
// Driver Code
$x1 = 3; $y1 = 2; $x2 = 15; $y2 = 5;
bresenham($x1, $y1, $x2, $y2);
 
// This code is contributed by nitin mittal.
?>

Javascript

<script>
 
// javascript program for Bresenhams Line Generation
// Assumptions :
// 1) Line is drawn from left to right.
// 2) x1 < x2 and y1 < y2
// 3) Slope of the line is between 0 and 1.
// We draw a line from lower left to upper
// right.
 
    // function for line generation
    function bresenham(x1 , y1 , x2,y2)
    {
        var m_new = 2 * (y2 - y1);
        var slope_error_new = m_new - (x2 - x1);
     
        for (x = x1, y = y1; x <= x2; x++)
        {
            document.write("(" +x + "," + y + ")<br>");
 
            // Add slope to increment angle formed
            slope_error_new += m_new;
 
            // Slope error reached limit, time to
            // increment y and update slope error.
            if (slope_error_new >= 0)
            {
                y++;
                slope_error_new -= 2 * (x2 - x1);
            }
        }
    }        
 
    // Driver code
 
var x1 = 3, y1 = 2, x2 = 15, y2 = 5;   
bresenham(x1, y1, x2, y2);
 
// This code is contributed by Amit Katiyar
 
</script>

Выход :

 (3,2)
(4,3)
(5,3)
(6,3)
(7,3)
(8,4)
(9,4)
(10,4)
(11,4)
(12,5)
(13,5)
(14,5)
(15,5)

Приведенное выше объяснение дает приблизительное представление об алгоритме. Для подробного объяснения и доказательства читатели могут обратиться к приведенным ниже ссылкам.
Статьи по Теме:

  1. Алгоритм создания линии средней точки
  2. Алгоритм DDA для рисования линий

Ссылка :
https://csustan.csustan.edu/~tom/Lecture-Notes/Graphics/Bresenham-Line/Bresenham-Line.pdf
https://en.wikipedia.org/wiki/Bresenham's_line_algorithm
http://graphics.idav.ucdavis.edu/education/GraphicsNotes/Bresenhams-Algorithm.pdf
Эта статья предоставлена Шивамом Прадханом (anuj_charm). Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью на сайте deposit.geeksforgeeks.org или отправить свою статью по электронной почте: grant@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

Алгоритмы Компьютерная графика

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Разница между жадным алгоритмом и алгоритмом «разделяй и властвуй»
14 Февраля, 2023
Сжатие и распаковка текстовых файлов с использованием кодирования Хаффмана
21 Января, 2023
Введение в амортизированный анализ
12 Января, 2023
Как анализировать сложность рекуррентного отношения
12 Января, 2023
Наихудший, средний и лучший анализ алгоритмов
4 Января, 2023
Лист Google SDE: вопросы и ответы на собеседовании
12 Декабря, 2022
Что такое логарифмическая временная сложность? Полное руководство
12 Декабря, 2022
Amazon SDE Sheet: вопросы и ответы на собеседовании
12 Декабря, 2022