Алгоритм Дулитла: разложение LU

Опубликовано: 18 Января, 2022

В численном анализе и линейной алгебре LU-разложение (где LU означает «нижний верхний» и также называется LU-факторизацией) факторизует матрицу как произведение нижней треугольной матрицы и верхней треугольной матрицы. Компьютеры обычно решают квадратные системы линейных уравнений с использованием LU-разложения, и это также является ключевым шагом при обращении матрицы или вычислении определителя матрицы. LU-разложение было введено математиком Тадеушем Банахевичем в 1938 году.

Пусть A - квадратная матрица. Факторизация LU относится к факторизации A с правильным порядком строк и / или столбцов или перестановками на два фактора: нижнюю треугольную матрицу L и верхнюю треугольную матрицу U, A = LU .

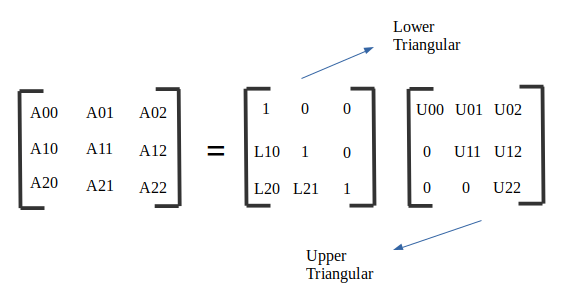
Алгоритм Дулитла :
Всегда можно разложить квадратную матрицу на нижнюю треугольную матрицу и верхнюю треугольную матрицу. То есть [A] = [L] [U]
Метод Дулитла предоставляет альтернативный способ разложить A на LU-разложение, не прибегая к хлопотам с исключением Гаусса.
Для общей матрицы A размера n × n мы предполагаем, что существует LU-разложение, и явно записываем форму L и U. Затем мы систематически решаем элементы в L и U из уравнений, которые возникают в результате умножений, необходимых для A = LU.

Термины матрицы U даются как:

И условия для L-матрицы: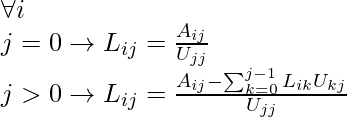

Пример :

 Вход :

Выход :

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

C++

// C++ Program to decompose a matrix into
// lower and upper traingular matrix
#include <bits/stdc++.h>
using namespace std;
 
const int MAX = 100;
 
void luDecomposition(int mat[][MAX], int n)
{
    int lower[n][n], upper[n][n];
    memset(lower, 0, sizeof(lower));
    memset(upper, 0, sizeof(upper));
 
    // Decomposing matrix into Upper and Lower
    // triangular matrix
    for (int i = 0; i < n; i++)
    {
        // Upper Triangular
        for (int k = i; k < n; k++)
        {
            // Summation of L(i, j) * U(j, k)
            int sum = 0;
            for (int j = 0; j < i; j++)
                sum += (lower[i][j] * upper[j][k]);
 
            // Evaluating U(i, k)
            upper[i][k] = mat[i][k] - sum;
        }
 
        // Lower Triangular
        for (int k = i; k < n; k++)
        {
            if (i == k)
                lower[i][i] = 1; // Diagonal as 1
            else
            {
                // Summation of L(k, j) * U(j, i)
                int sum = 0;
                for (int j = 0; j < i; j++)
                    sum += (lower[k][j] * upper[j][i]);
 
                // Evaluating L(k, i)
                lower[k][i]
                    = (mat[k][i] - sum) / upper[i][i];
            }
        }
    }
 
    // setw is for displaying nicely
    cout << setw(6)
         << "      Lower Triangular"
         << setw(32)
         << "Upper Triangular" << endl;
 
    // Displaying the result :
    for (int i = 0; i < n; i++)
    {
        // Lower
        for (int j = 0; j < n; j++)
            cout << setw(6) << lower[i][j] << "	";
        cout << "	";
 
        // Upper
        for (int j = 0; j < n; j++)
            cout << setw(6) << upper[i][j] << "	";
        cout << endl;
    }
}
 
// Driver code
int main()
{
    int mat[][MAX]
        = { { 2, -1, -2 }, { -4, 6, 3 }, { -4, -2, 8 } };
 
    luDecomposition(mat, 3);
    return 0;
}

Java

// Java Program to decompose a matrix into
// lower and upper traingular matrix
class GFG {
 
    static int MAX = 100;
    static String s = "";
    static void luDecomposition(int[][] mat, int n)
    {
        int[][] lower = new int[n][n];
        int[][] upper = new int[n][n];
 
        // Decomposing matrix into Upper and Lower
        // triangular matrix
        for (int i = 0; i < n; i++)
        {
            // Upper Triangular
            for (int k = i; k < n; k++)
            {
                // Summation of L(i, j) * U(j, k)
                int sum = 0;
                for (int j = 0; j < i; j++)
                    sum += (lower[i][j] * upper[j][k]);
 
                // Evaluating U(i, k)
                upper[i][k] = mat[i][k] - sum;
            }
 
            // Lower Triangular
            for (int k = i; k < n; k++)
            {
                if (i == k)
                    lower[i][i] = 1; // Diagonal as 1
                else
                {
                    // Summation of L(k, j) * U(j, i)
                    int sum = 0;
                    for (int j = 0; j < i; j++)
                        sum += (lower[k][j] * upper[j][i]);
 
                    // Evaluating L(k, i)
                    lower[k][i]
                        = (mat[k][i] - sum) / upper[i][i];
                }
            }
        }
 
        // setw is for displaying nicely
        System.out.println(setw(2) + "     Lower Triangular"
                           + setw(10) + "Upper Triangular");
 
        // Displaying the result :
        for (int i = 0; i < n; i++)
        {
            // Lower
            for (int j = 0; j < n; j++)
                System.out.print(setw(4) + lower[i][j]
                                 + "	");
            System.out.print("	");
 
            // Upper
            for (int j = 0; j < n; j++)
                System.out.print(setw(4) + upper[i][j]
                                 + "	");
            System.out.print("
");
        }
    }
    static String setw(int noOfSpace)
    {
        s = "";
        for (int i = 0; i < noOfSpace; i++)
            s += " ";
        return s;
    }
 
    // Driver code
    public static void main(String arr[])
    {
        int mat[][] = { { 2, -1, -2 },
                        { -4, 6, 3 },
                        { -4, -2, 8 } };
 
        luDecomposition(mat, 3);
    }
}
 
/* This code contributed by PrinciRaj1992 */

Python3

# Python3 Program to decompose
# a matrix into lower and
# upper traingular matrix
MAX = 100
 
 
def luDecomposition(mat, n):
 
    lower = [[0 for x in range(n)]
             for y in range(n)]
    upper = [[0 for x in range(n)]
             for y in range(n)]
 
    # Decomposing matrix into Upper
    # and Lower triangular matrix
    for i in range(n):
 
        # Upper Triangular
        for k in range(i, n):
 
            # Summation of L(i, j) * U(j, k)
            sum = 0
            for j in range(i):
                sum += (lower[i][j] * upper[j][k])
 
            # Evaluating U(i, k)
            upper[i][k] = mat[i][k] - sum
 
        # Lower Triangular
        for k in range(i, n):
            if (i == k):
                lower[i][i] = 1  # Diagonal as 1
            else:
 
                # Summation of L(k, j) * U(j, i)
                sum = 0
                for j in range(i):
                    sum += (lower[k][j] * upper[j][i])
 
                # Evaluating L(k, i)
                lower[k][i] = int((mat[k][i] - sum) /
                                  upper[i][i])
 
    # setw is for displaying nicely
    print("Lower Triangular		Upper Triangular")
 
    # Displaying the result :
    for i in range(n):
 
        # Lower
        for j in range(n):
            print(lower[i][j], end="	")
        print("", end="	")
 
        # Upper
        for j in range(n):
            print(upper[i][j], end="	")
        print("")
 
 
# Driver code
mat = [[2, -1, -2],
       [-4, 6, 3],
       [-4, -2, 8]]
 
luDecomposition(mat, 3)
 
# This code is contributed by mits

C#

// C# Program to decompose a matrix into
// lower and upper traingular matrix
using System;
 
class GFG {
 
    static int MAX = 100;
    static String s = "";
    static void luDecomposition(int[, ] mat, int n)
    {
        int[, ] lower = new int[n, n];
        int[, ] upper = new int[n, n];
 
        // Decomposing matrix into Upper and Lower
        // triangular matrix
        for (int i = 0; i < n; i++)
        {
            // Upper Triangular
            for (int k = i; k < n; k++)
            {
                // Summation of L(i, j) * U(j, k)
                int sum = 0;
                for (int j = 0; j < i; j++)
                    sum += (lower[i, j] * upper[j, k]);
 
                // Evaluating U(i, k)
                upper[i, k] = mat[i, k] - sum;
            }
 
            // Lower Triangular
            for (int k = i; k < n; k++)
            {
                if (i == k)
                    lower[i, i] = 1; // Diagonal as 1
                else
                {
                    // Summation of L(k, j) * U(j, i)
                    int sum = 0;
                    for (int j = 0; j < i; j++)
                        sum += (lower[k, j] * upper[j, i]);
 
                    // Evaluating L(k, i)
                    lower[k, i]
                        = (mat[k, i] - sum) / upper[i, i];
                }
            }
        }
 
        // setw is for displaying nicely
        Console.WriteLine(setw(2) + "     Lower Triangular"
                          + setw(10) + "Upper Triangular");
 
        // Displaying the result :
        for (int i = 0; i < n; i++)
        {
            // Lower
            for (int j = 0; j < n; j++)
                Console.Write(setw(4) + lower[i, j] + "	");
            Console.Write("	");
 
            // Upper
            for (int j = 0; j < n; j++)
                Console.Write(setw(4) + upper[i, j] + "	");
            Console.Write("
");
        }
    }
    static String setw(int noOfSpace)
    {
        s = "";
        for (int i = 0; i < noOfSpace; i++)
            s += " ";
        return s;
    }
 
    // Driver code
    public static void Main(String[] arr)
    {
        int[, ] mat = { { 2, -1, -2 },
                        
            

                    
                                    
РЕКОМЕНДУЕМЫЕ СТАТЬИ
                                    