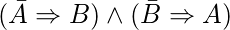2-удовлетворительная (2-SAT) проблема

Опубликовано: 25 Января, 2022

Проблема логической выполнимости

Boolean Satisfiability или просто SAT - это проблема определения, является ли логическая формула выполнимой или невыполнимой.

  • Выполнимость: если булевым переменным можно присвоить такие значения, что формула оказывается ИСТИННОЙ, то мы говорим, что формула выполнима.
  • Неудовлетворительно: если невозможно присвоить такие значения, мы говорим, что формула невыполнима.

Примеры:

  • , выполнимо, потому что A = TRUE и B = FALSE делает F = TRUE.
  • , является неудовлетворительным, потому что:
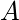ПРАВДА ЛОЖНЫЙ ЛОЖНЫЙ
ЛОЖНЫЙ ПРАВДА ЛОЖНЫЙ

Примечание: проблема булевой выполнимости является NP-полной (см. Теорему Кука).

Что такое 2-SAT Problem

2-SAT is a special case of Boolean Satisfiability Problem and can be solved 
in polynomial time.

Чтобы лучше понять это, сначала давайте посмотрим, что такое конъюнктивная нормальная форма (CNF) или также известная как произведение сумм (POS).
CNF: CNF - это соединение (И) предложений, где каждое предложение является дизъюнкцией (ИЛИ).
Теперь 2-SAT ограничивает проблему SAT только теми логическими формулами, которые выражаются как CNF, где каждое предложение имеет только 2 члена (также называемое 2-CNF ).
Пример:
Таким образом, Проблему 2-удовлетворенности можно сформулировать как:
Учитывая CNF с каждым предложением, имеющим только 2 члена, возможно ли присвоить такие значения переменным, чтобы CNF была ИСТИНА?
Примеры:

 Вход : 
Вывод: данное выражение выполнимо. 
(если x1 = ЛОЖЬ, x2 = ИСТИНА)
Вход : 
Вывод: данное выражение невыполнимо. 
(для всех возможных комбинаций x1 и x2)
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход к задаче 2-SAT

Чтобы значение CNF стало ИСТИНА, значение каждого предложения должно быть ИСТИНА. Пусть один из пунктов будет .

 *** QuickLaTeX не может составить формулу:


*** Сообщение об ошибке:
Ошибка: ничего не отображается, формула пуста

= ИСТИНА

  • Если A = 0, B должно быть 1, т.е.
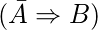
  • Если B = 0, A должно быть 1, т.е.

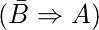
Таким образом, 

 = ИСТИНА эквивалентно

Теперь мы можем выразить CNF как следствие. Итак, мы создаем граф импликации, который имеет 2 ребра для каждого предложения CNF.
выражается в графе импликации как
Таким образом, для булевой формулы с предложениями 'm' мы создаем график импликации с:

  • 2 ребра для каждого пункта, т.е. ребра «2 м».
  • 1 узел для каждой логической переменной, входящей в логическую формулу.

Давайте посмотрим на один пример графа импликации.

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

Примечание: импликация (если A, то B) эквивалентна ее контрапозитиву (если тогда ).
Теперь рассмотрим следующие случаи:

 СЛУЧАЙ 1: Если  [Tex] существует в графе [/ Tex]
Это означает 
Если X = ИСТИНА,  = ИСТИНА, противоречие.
Но если X = FALSE, импликационных ограничений нет.
Таким образом, X = FALSE

СЛУЧАЙ 2: Если  [Tex] существует в графе [/ Tex]
Это означает 
Если  = ИСТИНА, X = ИСТИНА, противоречие.
Но если  = FALSE, импликационных ограничений нет.
Таким образом,  = ЛОЖЬ, т.е. X = ИСТИНА

СЛУЧАЙ 3: Если  [Tex] оба существуют в графе [/ Tex]
Одно ребро требует, чтобы X было ИСТИННО, а другое требует, чтобы X было ЛОЖЬ.
Таким образом, в таком случае переуступка невозможна.

CONCLUSION: If any two variables 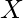and 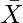are on a cycle i.e. both exists, then the CNF is unsatisfiable. Otherwise, there is a possible assignment and the CNF is satisfiable. 
Note here that, we use path due to the following property of implication: 
If we have 
Thus, if we have a path in the Implication Graph, that is pretty much same as having a direct edge.
CONCLUSION FROM IMPLEMENTATION POINT OF VIEW: 
If both X and 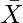lie in the same SCC (Strongly Connected Component), the CNF is unsatisfiable. 
A Strongly Connected Component of a directed graph has nodes such that every node can be reach from every another node in that SCC. 
Now, if X and 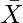lie on the same SCC, we will definitely have present and hence the conclusion.
Checking of the SCC can be done in O(E+V) using the Kosaraju’s Algorithm
 

C++

// C++ implementation to find if the given
// expression is satisfiable using the
// Kosaraju"s Algorithm
#include <bits/stdc++.h>
using namespace std;
 
const int MAX = 100000;
 
// data structures used to implement Kosaraju"s
// Algorithm. Please refer
// http://www.geeksforgeeks.org/strongly-connected-components/
vector<int> adj[MAX];
vector<int> adjInv[MAX];
bool visited[MAX];
bool visitedInv[MAX];
stack<int> s;
 
// this array will store the SCC that the
// particular node belongs to
int scc[MAX];
 
// counter maintains the number of the SCC
int counter = 1;
 
// adds edges to form the original graph
void addEdges(int a, int b)
{
    adj[a].push_back(b);
}
 
// add edges to form the inverse graph
void addEdgesInverse(int a, int b)
{
    adjInv[b].push_back(a);
}
 
// for STEP 1 of Kosaraju"s Algorithm
void dfsFirst(int u)
{
    if(visited[u])
        return;
 
    visited[u] = 1;
 
    for (int i=0;i<adj[u].size();i++)
        dfsFirst(adj[u][i]);
 
    s.push(u);
}
 
// for STEP 2 of Kosaraju"s Algorithm
void dfsSecond(int u)
{
    if(visitedInv[u])
        return;
 
    visitedInv[u] = 1;
 
    for (int i=0;i<adjInv[u].size();i++)
        dfsSecond(adjInv[u][i]);
 
    scc[u] = counter;
}
 
// function to check 2-Satisfiability
void is2Satisfiable(int n, int m, int a[], int b[])
{
    // adding edges to the graph
    for(int i=0;i<m;i++)
    {
        // variable x is mapped to x
        // variable -x is mapped to n+x = n-(-x)
 
        // for a[i] or b[i], addEdges -a[i] -> b[i]
        // AND -b[i] -> a[i]
        if (a[i]>0 && b[i]>0)
        {
            addEdges(a[i]+n, b[i]);
            addEdgesInverse(a[i]+n, b[i]);
            addEdges(b[i]+n, a[i]);
            addEdgesInverse(b[i]+n, a[i]);
        }
 
        else if (a[i]>0 && b[i]<0)
        {
            addEdges(a[i]+n, n-b[i]);
            addEdgesInverse(a[i]+n, n-b[i]);
            addEdges(-b[i], a[i]);
            addEdgesInverse(-b[i], a[i]);
        }
 
        else if (a[i]<0 && b[i]>0)
        {
            addEdges(-a[i], b[i]);
            addEdgesInverse(-a[i], b[i]);
            addEdges(b[i]+n, n-a[i]);
            addEdgesInverse(b[i]+n, n-a[i]);
        }
 
        else
        {
            addEdges(-a[i], n-b[i]);
            addEdgesInverse(-a[i], n-b[i]);
            addEdges(-b[i], n-a[i]);
            addEdgesInverse(-b[i], n-a[i]);
        }
    }
 
    // STEP 1 of Kosaraju"s Algorithm which
    // traverses the original graph
    for (int i=1;i<=2*n;i++)
        if (!visited[i])
            dfsFirst(i);
 
    // STEP 2 pf Kosaraju"s Algorithm which
    // traverses the inverse graph. After this,
    // array scc[] stores the corresponding value
    while (!s.empty())
    {
        int n = s.top();
        s.pop();
 
        if (!visitedInv[n])
        {
            dfsSecond(n);
            counter++;
        }
    }
 
    for (int i=1;i<=n;i++)
    {
        // for any 2 vairable x and -x lie in
        // same SCC
        if(scc[i]==scc[i+n])
        {
            cout << "The given expression "
                 "is unsatisfiable." << endl;
            return;
        }
    }
 
    // no such variables x and -x exist which lie
    // in same SCC
    cout << "The given expression is satisfiable."
         << endl;
    return;
}
 
//  Driver function to test above functions
int main()
{
    // n is the number of variables
    // 2n is the total number of nodes
    // m is the number of clauses
    int n = 5, m = 7;
 
    // each clause is of the form a or b
    // for m clauses, we have a[m], b[m]
    // representing a[i] or b[i]
 
    // Note:
    // 1 <= x <= N for an uncomplemented variable x
    // -N <= x <= -1 for a complemented variable x
    // -x is the complement of a variable x
 
    // The CNF being handled is:
    // "+" implies "OR" and "*" implies "AND"
    // (x1+x2)*(x2’+x3)*(x1’+x2’)*(x3+x4)*(x3’+x5)*
    // (x4’+x5’)*(x3’+x4)
    int a[] = {1, -2, -1, 3, -3, -4, -3};
    int b[] = {2, 3, -2, 4, 5, -5, 4};
 
    // We have considered the same example for which
    // Implication Graph was made
    is2Satisfiable(n, m, a, b);
 
    return 0;
}

Java

// Java implementation to find if the given
// expression is satisfiable using the
// Kosaraju"s Algorithm
import java.io.*;
import java.util.*;
 
class GFG{
 
static final int MAX = 100000;
 
// Data structures used to implement Kosaraju"s
// Algorithm. Please refer
// http://www.geeksforgeeks.org/strongly-connected-components/
@SuppressWarnings("unchecked")
static List<List<Integer> > adj = new ArrayList();
 
@SuppressWarnings("unchecked")
static List<List<Integer> > adjInv = new ArrayList();
static boolean[] visited = new boolean[MAX];
static boolean[] visitedInv = new boolean[MAX];
static Stack<Integer> s = new Stack<Integer>();
 
// This array will store the SCC that the
// particular node belongs to
static int[] scc = new int[MAX];
 
// counter maintains the number of the SCC
static int counter = 1;
 
// Adds edges to form the original graph void
static void addEdges(int a, int b)
{
    adj.get(a).add(b);
}
 
// Add edges to form the inverse graph
static void addEdgesInverse(int a, int b)
{
    adjInv.get(b).add(a);
}
 
// For STEP 1 of Kosaraju"s Algorithm
static void dfsFirst(int u)
{
    if (visited[u])
        return;
 
    visited[u] = true;
 
    for(int i = 0; i < adj.get(u).size(); i++)
        dfsFirst(adj.get(u).get(i));
 
    s.push(u);
}
 
// For STEP 2 of Kosaraju"s Algorithm
static void dfsSecond(int u)
{
    if (visitedInv[u])
        return;
 
    visitedInv[u] = true;
 
    for(int i = 0; i < adjInv.get(u).size(); i++)
        dfsSecond(adjInv.get(u).get(i));
 
    scc[u] = counter;
}
 
// Function to check 2-Satisfiability
static void is2Satisfiable(int n, int m,
                           int a[], int b[])
{
     
    // Adding edges to the graph
    for(int i = 0; i < m; i++)
    {
         
        // variable x is mapped to x
        // variable -x is mapped to n+x = n-(-x)
 
        // for a[i] or b[i], addEdges -a[i] -> b[i]
        // AND -b[i] -> a[i]
        if (a[i] > 0 && b[i] > 0)
        {
            addEdges(a[i] + n, b[i]);
            addEdgesInverse(a[i] + n, b[i]);
            addEdges(b[i] + n, a[i]);
            addEdgesInverse(b[i] + n, a[i]);
        }
 
        else if (a[i] > 0 && b[i] < 0)
        {
            addEdges(a[i] + n, n - b[i]);
            addEdgesInverse(a[i] + n, n - b[i]);
            addEdges(-b[i], a[i]);
            addEdgesInverse(-b[i], a[i]);
        }
 
        else if (a[i] < 0 && b[i] > 0)
        {
            addEdges(-a[i], b[i]);
            addEdgesInverse(-a[i], b[i]);
            addEdges(b[i] + n, n - a[i]);
            addEdgesInverse(b[i] + n, n - a[i]);
        }
 
        else
        {
            addEdges(-a[i], n - b[i]);
            addEdgesInverse(-a[i], n - b[i]);
            addEdges(-b[i], n - a[i]);
            addEdgesInverse(-b[i], n - a[i]);
        }
    }
 
    // STEP 1 of Kosaraju"s Algorithm which
    // traverses the original graph
    for(int i = 1; i <= 2 * n; i++)
        if (!visited[i])
            dfsFirst(i);
 
    // STEP 2 pf Kosaraju"s Algorithm which
    // traverses the inverse graph. After this,
    // array scc[] stores the corresponding value
    while (!s.isEmpty())
    {
        int top = s.peek();
        s.pop();
 
        if (!visitedInv[top])
        {
            dfsSecond(top);
            counter++;
        }
    }
 
    for(int i = 1; i <= n; i++)
    {
         
        // For any 2 vairable x and -x lie in
        // same SCC
        if (scc[i] == scc[i + n])
        {
            System.out.println("The given expression" +
                               "is unsatisfiable.");
            return;
        }
    }
 
    // No such variables x and -x exist which lie
    // in same SCC
    System.out.println("The given expression " +
                       "is satisfiable.");
}
 
// Driver code
public static void main(String[] args)
{
     
    // n is the number of variables
    // 2n is the total number of nodes
    // m is the number of clauses
    int n = 5, m = 7;
 
    for(int i = 0; i < MAX; i++)
    {
        adj.add(new ArrayList<Integer>());
        adjInv.add(new ArrayList<Integer>());
    }

РЕКОМЕНДУЕМЫЕ СТАТЬИ