Тест Колмогорова-Смирнова в программировании на R
Тест Колмогорова-Смирнова - это тип непараметрического теста на равенство прерывного и непрерывного одномерного распределения вероятностей, который используется для сравнения выборки с эталонным вероятностным тестом (известным как одновыборочный тест KS) или между двумя выборками. (известный как двухвыборочный тест KS). Тест KS количественно определяет расстояние между кумулятивной функцией распределения данного эталонного распределения и эмпирическими распределениями данных двух выборок или между эмпирическим распределением данных двух выборок. В тесте KS с одной выборкой распределение, которое рассматривается при нулевой гипотезе, может быть чисто дискретным, непрерывным или смешанным. В двухвыборочном KS-тесте распределение, рассматриваемое при нулевой гипотезе, обычно является непрерывным распределением, но в противном случае оно не ограничено. Тест Колмогорова-Смирнова можно очень легко выполнить в R Programming.
Формула теста Колмогорова-Смирнова
Формулу теста Колмогорова-Смирнова можно представить в виде:
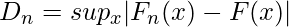
where,
supx : the supremum of the set of distances
Fn(x) : the empirical distribution function for n id observations Xi
Эмпирическая функция распределения - это функция распределения, которая связана с эмпирическими показателями выбранной выборки. Это кумулятивное распределение, являющееся ступенчатой функцией, увеличивается на шаг 1 / n для каждой n точек данных.
Реализация в R
Тест KS можно выполнить с помощью функции ks.test () в R.
Syntax:
ks.text(x, y, …, alternative = c(“two.sided”, “less”, “greater”), exact= NULL, tol= 1e-8,
simulate.p.value = FALSE, B=2000)Parameters:
x: numeric vector of data values
y: numeric vector of data values or a character string which is used to name a cummulative distribution function.
…: the parameters which are defined by the y valuealternative: used to indicate the alternate hypothesis.
exact: usually NULL or it indicates a logic that an exact p-value should be computed.tol: an upper bound used for rounding off errors in the data values.
simulate.p.value: a logic that checks whether to use Monte Carlo method to compute the p-value.
B: an integer value that indicates the number of replicates to be created while using the Monte Carlo method.
Давайте разберемся, как выполнить тест KS пошагово на примере двухвыборочного теста KS.
- Шаг 1: Сначала установите необходимые пакеты . Для выполнения теста KS нам необходимо установить пакет «dgof » с помощью функции install.packages () из консоли R.
install.packages ("dgof")
- Шаг 2: После успешной установки пакета загрузите требуемый пакет в наш R Script. для этой цели используйте функцию library () следующим образом:
р
# loading the required packagelibrary ( "dgof" ) |
- Шаг 3: Используйте функцию rnorm () и функцию runif (), чтобы сгенерировать образцы, скажем, x и y. Функция rnorm () используется для генерации случайных значений, а функция runif () используется для генерации случайных отклонений.
р
# loading the required packagelibrary (dgof) # generating random variate# sample 1x <- rnorm (50) # generating random deviates# sample 2y <- runif (30) |
- Шаг 4: Теперь проведите тест KS на этих двух образцах. Для этого используйте ks.test () пакета dgof.
р
# loading the required packagelibrary (dgof) # generating random variate# sample 1x <- rnorm (50) # generating random deviates# sample 2y <- runif (30) # performing the KS Test# Do x and y come from# the same distribution?ks.test (x, y) |
Выход:
Двухвыборочный критерий Колмогорова-Смирнова данные: x и y D = 0,84, значение p = 5,151e-14 альтернативная гипотеза: двусторонняя
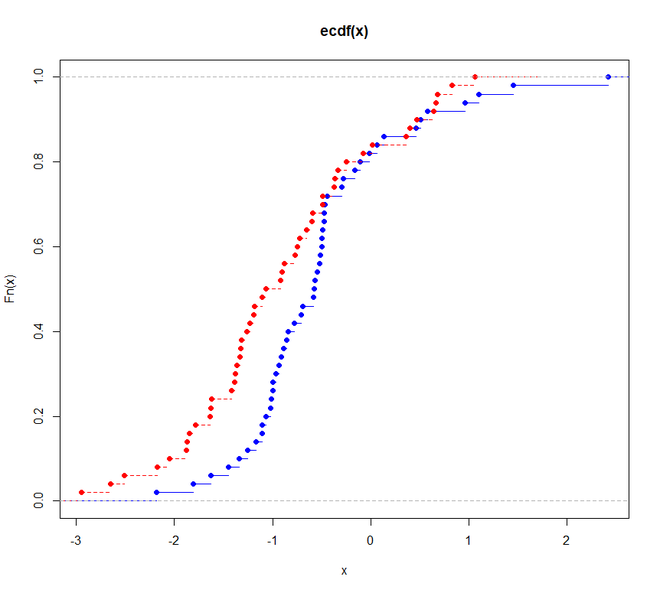
Визуализация теста Колмогорова-Смирнова в R
Будучи весьма чувствительным к разнице формы и местоположения эмпирического кумулятивного распределения двух выбранных выборок, двухвыборочный тест KS является эффективным и одним из наиболее общих и полезных непараметрических тестов. Следовательно, мы увидим, как график представляет разницу между двумя образцами.
Пример:
Здесь мы генерируем оба образца с помощью функции rnorm (), а затем строим их.
р
# loading the required packagelibrary (dgof) # sample 1# generating a random variatex <- rnorm (50) # sample 2# generating a random variatex2 <- rnorm (50, -1) # plotting the result# visualizationplot ( ecdf (x), xlim = range ( c (x, x2)), col = "blue" )plot ( ecdf (x2), add = TRUE , lty = "dashed" , col = "red" ) # performing the KS# Test on x and x2ks.test (x, x2, alternative = "l" ) |
Выход:
Двухвыборочный критерий Колмогорова-Смирнова данные: x и x2 D ^ - = 0,34, значение p = 0,003089 альтернативная гипотеза: CDF x лежит ниже CDF y