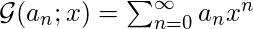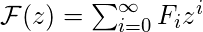Получение выражения чисел Фибоначчи в терминах золотого сечения

Предпосылки: генерирующие функции, числа Фибоначчи, методы поиска чисел Фибоначчи.

В этом посте обсуждался метод использования генерирующих функций для решения знаменитых и полезных повторений чисел Фибоначчи.

Генерирующая функция - это мощный инструмент для решения широкого круга математических задач, в том числе задач подсчета. Это формальный степенной ряд. Например, при подсчете задач нас часто интересует определение количества объектов размером 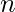. В таком случае мы определяем степенной ряд, который, говоря простым языком, представляет собой бесконечный многочлен, в котором коэффициент при 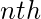термин степень 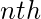член последовательности. Это помогает нам получить много интересных и важных результатов. Следует отметить, что при использовании производящих функций мы обычно используем коэффициенты в степенном ряду производящей функции, мы редко используем переменную в ряду. В этом посте мы сделаем то же самое. Обычная производящая функция некоторого a _n :

Числа Фибоначчи - одна из фундаментальных последовательностей в математике, и было обнаружено множество способов найти члены высшего порядка этой последовательности. В этом посте обсуждается один из таких методов.

Давайте сначала определим производящую функцию для чисел Фибоначчи, а затем функция будет упрощена, чтобы получить повторение. Используя это, расширьте упрощение и разбейте его на частичные дроби, а затем используйте два стандартных степенных ряда, а затем объедините их оба, чтобы получить удивительный результат для 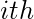член ряда Фибоначчи.

Определим производящую функцию 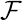в качестве

,

where is the ith Fibonacci Number.

С,

.

.

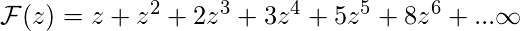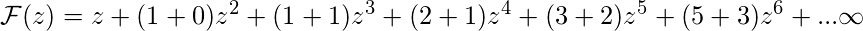Переставляя их, мы получаем,

.

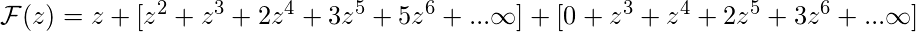Принимая общие термины,

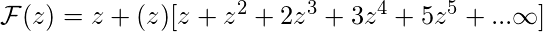
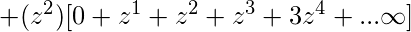
Дальнейшее упрощение дает следующую функцию.

.

Решение для 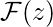, мы получаем:

.

С помощью вышеуказанных операций мы получаем формулу ниже:

,

where, and .

Таким образом,

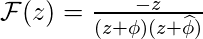
Также обратите внимание, что,

.

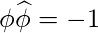Таким образом, сохраняя это соотношение в приведенном выше выражении, мы получаем,

.

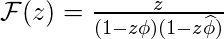Теперь правую часть приведенного выше выражения можно разделить на дробные части:

.

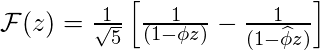Используя разложение на две фракции,

.

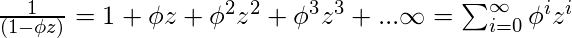Сходным образом,

.

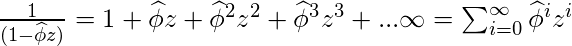Таким образом,

.

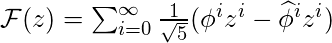Таким образом,

.

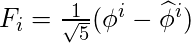Теперь,

,

а также,

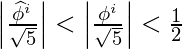
Используя два приведенных выше факта, можно с уверенностью заключить, что ценность

, rounded to the nearest integer.

Нахождение n-го числа Фибоначчи с использованием золотого сечения - одно из применений этой формулы.

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.