Паттерн филлотаксиса в Python | Блок алгоритмической ботаники

Опубликовано: 14 Июля, 2021

Филлотаксис / филлотаксия - это расположение листьев на стебле растения, а филлотактические спирали образуют особый класс узоров в природе. Само слово происходит от греческого phullon, что означает «лист», и taxis, что означает «композиция». Основные цветочные филлотаксические композиции включают:
1. Спиральное филлотаксис. При спиральной филлотаксии отдельные цветочные органы создаются через равные промежутки времени с одинаковым углом расхождения. Угол расхождения в цветке со спиральной филлотаксией составляет приблизительно 137,5 градусов, что свидетельствует о паттерне, который следует серии Фибоначчи . На изображении ниже показаны спиральные паттерны филлотаксии, имеющие спиральные узоры как по часовой, так и против часовой стрелки.

Важные моменты, на которые следует обратить внимание:

Ряды Фибоначчи обычно описывают спирали, встречающиеся в природе. Он рассчитывается как серия, в которой предыдущая пара чисел суммируется со следующим числом в серии. Серии 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89….
На самом деле существует один набор спиралей, вращающихся по часовой стрелке, и один набор - против часовой стрелки.
Спирали цветочных органов следуют за числителем и знаменателем набора смещенных чисел Фибоначчи (1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34…). Числитель - это количество раз или оборотов вокруг оси, чтобы вернуться в исходную точку. Знаменатель указывает количество органов, инициированных во время ходов. Следовательно, 2/5 будет означать 2 оборота вокруг оси и 5 органов, которые вернутся в исходное положение.
Например, у сосны есть филлотаксы (2, 3), (5, 3) и (5, 8), в capituli найдены пары (21, 34), (55, 34), (55, 89) , и (89, 144), а на ананасах с гексагональной чешуей встречаются тройки (8, 13, 21) или (13, 21, 34), в зависимости от размера экземпляров.
Преобладание последовательности Фибоначчи в филлотаксисе часто называют «загадкой филлотаксиса».

Другие типы цветочных филлотаксических композиций:
2. Филлотаксис с мутовками, 3. Филлотаксис с простыми мутовками, 4. Филлотаксис со сложными мутовками и 5. Нерегулярный филлотаксис.

Формирование паттерна: резюме

Красивое расположение листьев у некоторых растений, называемое филлотаксисом, подчиняется ряду тонких математических соотношений. Например, соцветия в головке подсолнечника образуют две противоположно направленных спирали: 55 из них по часовой стрелке и 34 против часовой стрелки. Удивительно,

Эти числа являются последовательными числами Фибоначчи.
Отношения альтернативных чисел Фибоначчи задаются приближающимися к φ ^ (- 2), где φ - золотое сечение, и, как говорят, измеряют долю оборота между последовательными листьями на стебле растения:
например: 1/2 для вяз и липы, 1/3 для бука и орешника, 2/5 для дуба и яблони, 3/8 для тополя и розы, 5/13 для ивы и миндаля и т. д.
Каждый новый лист на стебле растения расположен под определенным углом к предыдущему, и этот угол между листьями постоянен: обычно около 137,5 градусов.

То есть, если вы посмотрите сверху на растение и измерите угол, образованный линией, проведенной от стебля к листу, и соответствующей линией для следующего листа, вы обнаружите, что обычно существует фиксированный угол, называемый расхождением. угол.
Здесь нас интересует Спиральная филлотаксия, и мы создадим код для формирования паттерна Спиральная Филлотаксия в питоне с использованием графики черепахи.

Разработка кода

Мы будем кодировать две функции: одну для рисования паттерна филлотаксии, а другую - для рисования лепестков.
Лепестки нужно рисовать только после того, как шаблон филлотаксиса будет завершен. Итак, мы вызовем функцию drawPetal () изнутри функции drawPhyllPattern () с последними координатами x и y, которые были посещены после рисования шаблона филлотаксиса.
Функция drawPetal () будет рисовать лепестки с функциями и особенностями черепахи, см. Программирование черепахи.

Чтобы закодировать паттерн филлотаксиса, нам нужно следовать этим уравнениям:

х = г * соз (θ)
у = г * грех (θ)

r, θ также могут варьироваться - поэтому для формирования филлотактического паттерна мы подставляем декартову форму
по полярной форме:

г = с * sqrt (п)
θ = п * 137,508 °

Сводит проблему к оптимальной упаковке на диске, поэтому
    r = c * sqrt (n) от площади круга
        Площадь = πr² и n заполняет площадь в некоторых единицах.
        c1 * n / π = r², c равно 1 / sqrt (c1 / π)
Итак, r = некоторая константа c * sqrt (n)

Псевдокод: шаблон филлотаксиса

ИМПОРТ МОДУЛЕЙ (МАТЕМАТИКА, ЧЕРЕПАХА)

ФУНКЦИЯ - DrawPhyllotaxisPattern (черепаха, длина t, начало лепестка, угол = 137,508, размер, распространение)
    turtleColor ("Черный")
    FillColor ('"Оранжевый")
    Преобразовать угол в радианы (Φ)
    инициализировать (xcenter, ycenter) = (0,0)
    Рисование паттерна начинается:
    Для n в диапазоне (0, t):
        r = c распространением * sqrt (n)
        θ = n * Φ

        x = r * cos (θ) + xцентр
            y = r * sin (θ) + yцентр

        ПОЛОЖЕНИЕ ЧЕРЕПАХИ (x, y)
        НАЧАТЬ РИСОВАТЬ():
        если рисунок рисунка заканчивается:
            DrawFlowerPetals ()
 
ФУНКЦИЯ - DrawFlowerPetals (Черепаха, координата x, координата y)
    РИСОВАТЬ с использованием методов Черепахи

Создать черепаху = gfg
Вызов DrawPhyllotaxisPattern (gfg, t length, petalstart, angle = 137,508, size, c spread)

КОНЕЦ

Шаблон Python A

 import math
 import turtle
 
def drawPhyllPattern(turtle, t, petalstart, angle = 137.508 , size = 2 , cspread = 4 ):
    """print a pattern of circles using spiral phyllotactic data"""
    # initialize position
    # turtle.pen(outline=1, pencolor="black", fillcolor="orange")
    turtle.color( 'black' )
    turtle.fillcolor( "orange" )
    phi = angle * ( math.pi / 180.0 ) #we convert to radian
    xcenter = 0.0
    ycenter = 0.0
    
    # for loops iterate in this case from the first value until < 4, so
    for n in range ( 0 , t):
        r = cspread * math.sqrt(n)
        theta = n * phi
         
        x = r * math.cos(theta) + xcenter
        y = r * math.sin(theta) + ycenter
 
        # move the turtle to that position and draw
        turtle.up()
        turtle.setpos(x, y)
        turtle.down()
        # orient the turtle correctly
        turtle.setheading(n * angle)
        if n > petalstart - 1 :
            turtle.color( "yellow" )
            drawPetal(turtle, x, y)
        else : turtle.stamp()
             
 
def drawPetal(turtle, x, y ):
    turtle.penup()
    turtle.goto(x, y)
    turtle.pendown()
    turtle.color( 'black' )
    turtle.fillcolor( 'yellow' )
    turtle.begin_fill()
    turtle.right( 20 )
    turtle.forward( 70 )
    turtle.left( 40 )
    turtle.forward( 70 )
    turtle.left( 140 )
    turtle.forward( 70 )
    turtle.left( 40 )
    turtle.forward( 70 )
    turtle.penup()
    turtle.end_fill() # this is needed to complete the last petal
 
 
gfg = turtle.Turtle()
 gfg.shape( "turtle" )
 gfg.speed( 0 ) # make the turtle go as fast as possible
 drawPhyllPattern(gfg, 200 , 160 , 137.508 )
 gfg.penup()
 gfg.forward( 1000 ) 

Шаблон Python B

 import math
 import turtle
 
def drawPhyllotacticPattern( t, petalstart, angle = 137.508 , size = 2 , cspread = 4 ):
        """print a pattern of circles using spiral phyllotactic data"""
        # initialize position
        turtle.pen(outline = 1 , pencolor = "black" , fillcolor = "orange" )
        # turtle.color("orange")
        phi = angle * ( math.pi / 180.0 )
        xcenter = 0.0
        ycenter = 0.0
        
        # for loops iterate in this case from the first value until < 4, so
        for n in range ( 0 , t):
                r = cspread * math.sqrt(n)
                theta = n * phi
                 
                x = r * math.cos(theta) + xcenter
                y = r * math.sin(theta) + ycenter
  
                # move the turtle to that position and draw
                turtle.up()
                turtle.setpos(x, y)
                turtle.down()
                # orient the turtle correctly
                turtle.setheading(n * angle)
                if n > petalstart - 1 :
                        #turtle.color("yellow")
                        drawPetal(x, y)
                else : turtle.stamp()
                 
 
def drawPetal( x, y ):
        turtle.up()
        turtle.setpos(x, y)
        turtle.down()
        turtle.begin_fill()
        #turtle.fill(True)
        turtle.pen(outline = 1 , pencolor = "black" , fillcolor = "yellow" )
        turtle.right( 20 )
        turtle.forward( 100 )
        turtle.left( 40 )
        turtle.forward( 100 )
        turtle.left( 140 )
        turtle.forward( 100 )
        turtle.left( 40 )
        turtle.forward( 100 )
        turtle.up()
        turtle.end_fill() # this is needed to complete the last petal
 
 
 
turtle.shape( "turtle" )
 turtle.speed( 0 ) # make the turtle go as fast as possible
 drawPhyllotacticPattern( 200 , 160 , 137.508 , 4 , 10 )
 turtle.exitonclick() # lets you x out of the window when outside of idle 

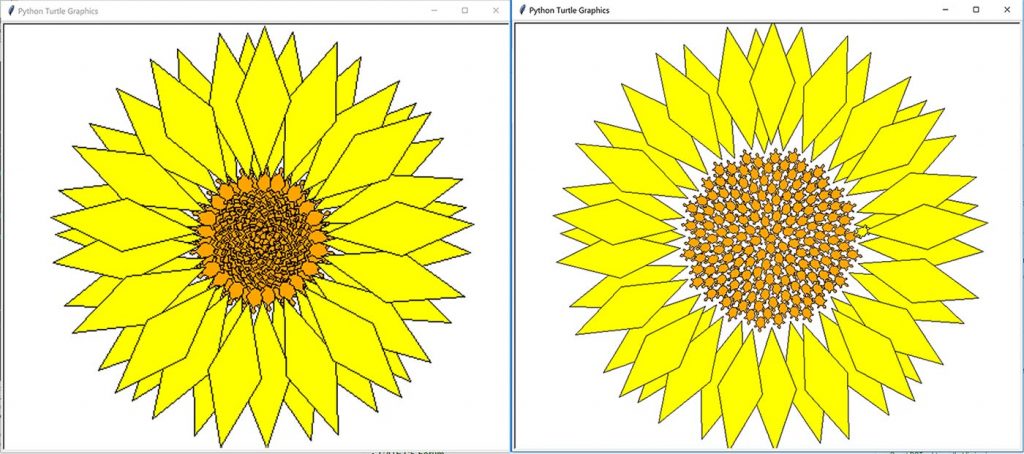
Продукт: паттерны филлотаксиса.

Источники:

Питон и графика черепахи Деборы Р. Фаулер
Филлотактический паттерн Деборы Р. Фаулер Реализация Python Деборой Р. Фаулер www.sciteneg.com/PhiTaxis/Phyllotaxis: The Fibonacci Sequence in Naturealgorithmicbotany.org

Эта статья предоставлена Amartya Ranjan Saikia. Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на deposit@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам. Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше. Мои личные заметки arrow_drop_upСохранить

Python Машинное обучение

Паттерн филлотаксиса в Python | Блок алгоритмической ботаники

Шаблон Python A

Шаблон Python B

РЕКОМЕНДУЕМЫЕ СТАТЬИ