ML | Использование SVM для классификации нелинейного набора данных

Опубликовано: 25 Июля, 2021

Предварительное условие: машины опорных векторов

Определение гиперплоскости и классификатора SVM:
Для линейно разделяемого набора данных, имеющего n объектов (что требует n измерений для представления), гиперплоскость в основном представляет собой (n - 1) размерное подпространство, используемое для разделения набора данных на два набора, каждый набор содержит точки данных, принадлежащие разному классу. Например, для набора данных, имеющего две характеристики X и Y (следовательно, лежащих в 2-мерном пространстве), разделяющая гиперплоскость представляет собой линию (одномерное подпространство). Точно так же для набора данных, имеющего 3 измерения, у нас есть 2-мерная разделяющая гиперплоскость и так далее.
В машинном обучении машина опорных векторов (SVM) - это не вероятностный линейный двоичный классификатор, используемый для классификации данных путем обучения гиперплоскости, разделяющей данные.

Классификация нелинейно разделяемого набора данных с помощью SVM - линейного классификатора:
Как упоминалось выше, SVM - это линейный классификатор, который изучает (n - 1) -мерный классификатор для классификации данных на два класса. Однако его можно использовать для классификации нелинейного набора данных. Это можно сделать, проецируя набор данных в более высокое измерение, в котором он может быть линейно разделен!

Чтобы лучше понять, давайте рассмотрим набор данных кругов.

 # importing libraries
 import numpy as np
 import matplotlib.pyplot as plt
 from sklearn.datasets import make_circles
 from mpl_toolkits.mplot3d import Axes3D
 
# generating data
 X, Y = make_circles(n_samples = 500 , noise = 0.02 )
 
# visualizing data
 plt.scatter(X[:, 0 ], X[:, 1 ], c = Y, marker = '.' )
 plt.show()

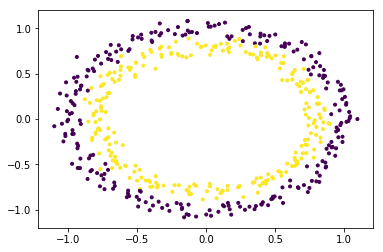
Набор данных явно является нелинейным набором данных и состоит из двух функций (скажем, X и Y).

Чтобы использовать SVM для классификации этих данных, введите в набор данных ^{еще одну функцию Z = X 2} + Y ^2. Таким образом, проецирование двумерных данных в трехмерное пространство. Первое измерение представляет объект X, второе представляет Y и третье представляет Z (который математически равен радиусу круга, частью которого является точка (x, y)). Теперь ясно, что для данных, показанных выше, «желтые» точки данных принадлежат кругу меньшего радиуса, а «фиолетовые» точки данных принадлежат кругу большего радиуса. Таким образом, данные становятся линейно разделяемыми по оси Z.

 # adding a new dimension to X
 X1 = X[:, 0 ].reshape(( - 1 , 1 ))
 X2 = X[:, 1 ].reshape(( - 1 , 1 ))
 X3 = (X1 * * 2 + X2 * * 2 )
 X = np.hstack((X, X3))
 
# visualizing data in higher dimension
 fig = plt.figure()
 axes = fig.add_subplot( 111 , projection = '3d' )
 axes.scatter(X1, X2, X1 * * 2 + X2 * * 2 , c = Y, depthshade = True )
 plt.show()

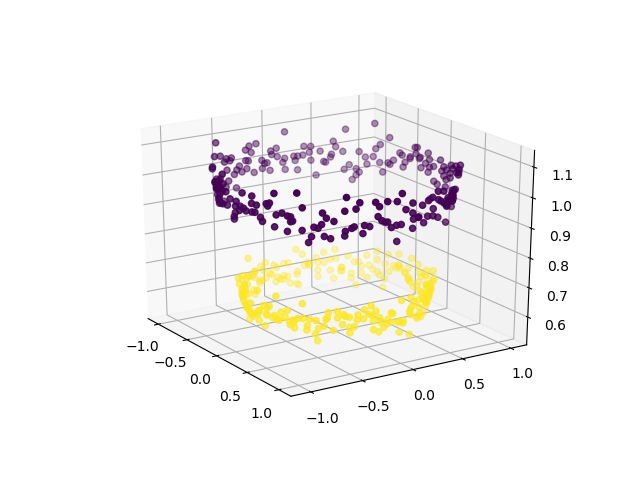
Теперь мы можем использовать SVM (или, если на то пошло, любой другой линейный классификатор), чтобы изучить 2-мерную разделяющую гиперплоскость. Вот как будет выглядеть гиперплоскость:

 # create support vector classifier using a linear kernel
 from sklearn import svm
 
svc = svm.SVC(kernel = 'linear' )
 svc.fit(X, Y)
 w = svc.coef_
 b = svc.intercept_
 
# plotting the separating hyperplane
 x1 = X[:, 0 ].reshape(( - 1 , 1 ))
 x2 = X[:, 1 ].reshape(( - 1 , 1 ))
 x1, x2 = np.meshgrid(x1, x2)
 x3 = - (w[ 0 ][ 0 ] * x1 + w[ 0 ][ 1 ] * x2 + b) / w[ 0 ][ 2 ]
 
fig = plt.figure()
 axes2 = fig.add_subplot( 111 , projection = '3d' )
 axes2.scatter(X1, X2, X1 * * 2 + X2 * * 2 , c = Y, depthshade = True )
 axes1 = fig.gca(projection = '3d' )
 axes1.plot_surface(x1, x2, x3, alpha = 0.01 )
 plt.show()

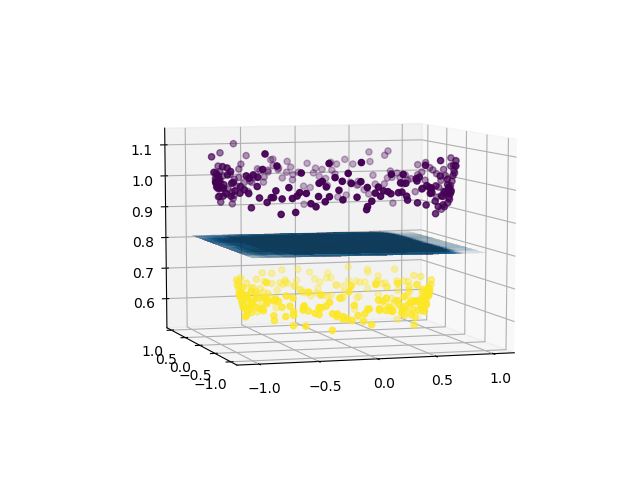
Таким образом, используя линейный классификатор, мы можем разделить нелинейно разделяемый набор данных.

Краткое введение в ядра в машинном обучении:
В машинном обучении трюк, известный как «уловка ядра», используется для изучения линейного классификатора для классификации нелинейного набора данных. Он преобразует линейно неразделимые данные в линейно разделимые, проецируя их в более высокое измерение. К каждому экземпляру данных применяется функция ядра, чтобы отобразить исходные нелинейные точки данных в некоторое пространство более высокой размерности, в котором они становятся линейно разделяемыми.

Машинное обучение Продвинутая компьютерная тематика

ML | Использование SVM для классификации нелинейного набора данных

РЕКОМЕНДУЕМЫЕ СТАТЬИ